Bingung dengan soal-soal matematika di halaman 92 buku pelajaran kelas 9? Tenang, kamu tidak sendirian! Banyak siswa yang merasa kesulitan memahami konsep dan menyelesaikan soal-soal di halaman tersebut. Artikel ini akan membahas kunci jawaban matematika kelas 9 halaman 92, mulai dari contoh soal, jenis soal, konsep matematika yang diulas, hingga strategi penyelesaian yang efektif.
Kamu akan menemukan penjelasan rinci tentang setiap konsep, contoh penerapannya dalam kehidupan sehari-hari, dan tips untuk menghindari kesalahan umum. Mari kita selami dunia matematika di halaman 92 dan temukan solusi yang tepat!
Soal-soal Matematika Kelas 9 Halaman 92

Halaman 92 buku pelajaran matematika kelas 9 biasanya berisi soal-soal yang menguji pemahaman siswa tentang materi tertentu. Soal-soal ini dapat berupa soal cerita, soal hitungan, atau soal yang menggabungkan keduanya. Tujuan dari soal-soal ini adalah untuk membantu siswa mengasah kemampuan berpikir kritis dan memecahkan masalah.
Contoh Soal Matematika Kelas 9 Halaman 92
Berikut ini adalah contoh tiga soal matematika yang mungkin terdapat pada halaman 92 buku pelajaran kelas 9.
- Sebuah persegi panjang memiliki panjang 12 cm dan lebar 8 cm. Hitunglah luas persegi panjang tersebut!
- Sebuah tabung memiliki jari-jari alas 7 cm dan tinggi 10 cm. Hitunglah volume tabung tersebut!
- Sebuah mobil melaju dengan kecepatan 60 km/jam. Berapa jarak yang ditempuh mobil tersebut dalam waktu 2 jam?
Jenis Soal Matematika pada Halaman 92
Jenis soal matematika yang terdapat pada halaman 92 buku pelajaran kelas 9 biasanya meliputi:
- Soal tentang bangun datar, seperti persegi panjang, segitiga, lingkaran, dan lainnya.
- Soal tentang bangun ruang, seperti kubus, balok, tabung, kerucut, dan bola.
- Soal tentang kecepatan, jarak, dan waktu.
- Soal tentang persamaan linear satu variabel.
Tabel Soal Matematika Kelas 9 Halaman 92
| Nomor Soal | Jenis Soal | Rumus yang Digunakan | Langkah Penyelesaian |
|---|---|---|---|
| 1 | Luas Persegi Panjang | Luas = panjang x lebar | Luas = 12 cm x 8 cm = 96 cm2 |
| 2 | Volume Tabung | Volume = π x r2 x t | Volume = 3,14 x 72 cm x 10 cm = 1538,6 cm3 |
| 3 | Jarak, Kecepatan, dan Waktu | Jarak = kecepatan x waktu | Jarak = 60 km/jam x 2 jam = 120 km |
Konsep Matematika yang Diulas

Halaman 92 buku matematika kelas 9 membahas tentang persamaan garis lurus. Konsep ini sangat penting karena menjadi dasar untuk memahami berbagai aplikasi matematika di kehidupan sehari-hari.
Persamaan Garis Lurus
Persamaan garis lurus adalah rumus matematika yang menggambarkan hubungan antara dua variabel, biasanya x dan y, yang membentuk garis lurus pada bidang koordinat. Persamaan garis lurus umumnya ditulis dalam bentuk:
y = mx + c
Butuh bantuan buat ngerjain soal-soal matematika kelas 9 halaman 92? Tenang, kamu gak sendirian! Banyak banget siswa yang ngalamin hal serupa. Tapi, jangan khawatir, banyak sumber belajar yang bisa kamu akses. Misalnya, kalau kamu butuh jawaban untuk soal-soal di halaman 20, kamu bisa cek di kunci jawaban matematika kelas 9 halaman 20.
Nah, setelah kamu memahami konsepnya, kamu bisa coba lagi untuk mengerjakan soal-soal di halaman 92. Ingat, kunci sukses belajar matematika adalah memahami konsep dan latihan rutin, bukan hanya sekadar mencari kunci jawaban. Semangat!
Dimana:* y adalah variabel dependen (sumbu vertikal)
- x adalah variabel independen (sumbu horizontal)
- m adalah gradien garis, yang menunjukkan kemiringan garis
- c adalah konstanta, yang menunjukkan titik potong garis dengan sumbu y.
Menentukan Persamaan Garis Lurus
Ada beberapa cara untuk menentukan persamaan garis lurus, yaitu:* Dengan Dua Titik:Jika diketahui dua titik yang dilalui oleh garis, kita dapat menentukan gradien dan konstanta dengan rumus:
m = (y2
- y1) / (x2
- x1)
dan kemudian substitusikan salah satu titik dan nilai gradien ke dalam persamaan y = mx + c untuk mendapatkan konstanta.* Dengan Gradien dan Titik:Jika diketahui gradien garis dan satu titik yang dilalui garis, kita dapat langsung substitusikan nilai gradien dan titik ke dalam persamaan y = mx + c untuk mendapatkan konstanta.* Dengan Bentuk Titik-Gradien:Bentuk titik-gradien adalah persamaan garis lurus yang ditulis dalam bentuk:
y
- y1 = m(x
- x1)
Dimana (x1, y1) adalah titik yang dilalui garis dan m adalah gradien.
Contoh Penerapan dalam Kehidupan Sehari-hari
Persamaan garis lurus memiliki banyak aplikasi dalam kehidupan sehari-hari, misalnya:* Menghitung Kecepatan:Jika kita mengetahui jarak yang ditempuh dan waktu yang diperlukan, kita dapat menghitung kecepatan dengan rumus:
Kecepatan = Jarak / Waktu
Rumus ini merupakan persamaan garis lurus dengan kecepatan sebagai variabel dependen, jarak sebagai variabel independen, dan gradien sebagai nilai kecepatan.* Menghitung Biaya:Jika kita ingin mengetahui biaya total untuk membeli sejumlah barang, kita dapat menggunakan persamaan garis lurus. Misalnya, jika harga satu barang adalah Rp10.000 dan kita membeli 5 barang, maka biaya totalnya adalah:
Biaya Total = (Harga per Barang) x (Jumlah Barang)
Rumus ini merupakan persamaan garis lurus dengan biaya total sebagai variabel dependen, jumlah barang sebagai variabel independen, dan harga per barang sebagai gradien.* Menghitung Suhu:Hubungan antara skala Celsius dan Fahrenheit dapat diwakili oleh persamaan garis lurus. Rumusnya adalah:
F = (9/5)C + 32
Dimana F adalah suhu dalam Fahrenheit dan C adalah suhu dalam Celsius.* Menghitung Profit:Dalam bisnis, persamaan garis lurus dapat digunakan untuk menghitung profit. Profit adalah selisih antara pendapatan dan biaya. Persamaan garis lurus dapat digunakan untuk menggambarkan hubungan antara pendapatan, biaya, dan profit.* Menghitung Konsumsi Energi:Persamaan garis lurus dapat digunakan untuk menghitung konsumsi energi.
Misalnya, jika kita mengetahui jumlah watt yang digunakan oleh suatu perangkat dan waktu penggunaan, kita dapat menghitung konsumsi energi dengan rumus:
Konsumsi Energi = (Watt) x (Waktu)
Rumus ini merupakan persamaan garis lurus dengan konsumsi energi sebagai variabel dependen, waktu sebagai variabel independen, dan watt sebagai gradien.
Kesimpulan
Persamaan garis lurus merupakan konsep matematika yang penting dan memiliki banyak aplikasi dalam kehidupan sehari-hari. Memahami konsep ini akan membantu kita dalam menyelesaikan berbagai masalah yang melibatkan hubungan antara dua variabel.
Strategi Menyelesaikan Soal
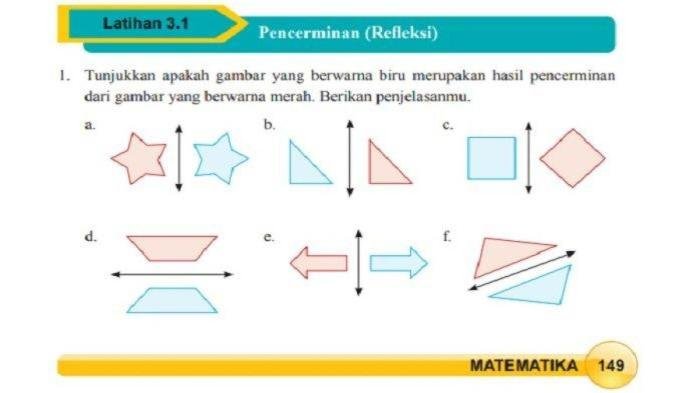
Menyelesaikan soal matematika di kelas 9, khususnya di halaman 92, memerlukan strategi yang tepat. Strategi yang tepat akan membantumu memahami konsep, mengidentifikasi informasi penting, dan menghindari kesalahan yang umum.
Memahami Konsep
Langkah pertama adalah memahami konsep yang diujikan dalam soal. Baca soal dengan cermat dan identifikasi kata kunci yang menunjukkan konsep yang diuji. Misalnya, jika soal membahas tentang persamaan linear, maka kamu perlu memahami cara menyelesaikan persamaan linear.
Lagi-lagi bingung sama soal matematika kelas 9 halaman 92? Tenang, banyak kok yang mengalami hal serupa! Kunci jawabannya pasti ada, tapi jangan lupa untuk memahami konsepnya juga ya. Kalau lagi belajar Bahasa Inggris, kamu bisa cek kunci jawaban bahasa inggris kelas 9 halaman 14 untuk membantu kamu dalam memahami materi.
Nah, setelah selesai belajar Bahasa Inggris, kembali lagi deh ke soal matematika kelas 9 halaman 92. Selamat belajar!
Menganalisis Soal, Kunci jawaban matematika kelas 9 halaman 92
Setelah memahami konsep, langkah selanjutnya adalah menganalisis soal. Identifikasi informasi yang diberikan dalam soal dan apa yang ditanyakan. Tuliskan informasi yang diberikan dalam bentuk yang mudah dipahami, seperti tabel atau diagram.
Menentukan Strategi Penyelesaian
Setelah menganalisis soal, tentukan strategi penyelesaian yang paling tepat. Ada beberapa strategi yang bisa kamu gunakan, seperti:
- Menggunakan rumus yang relevan
- Membuat diagram atau gambar untuk membantu visualisasi
- Menyederhanakan soal dengan menggunakan teknik substitusi atau eliminasi
- Memeriksa jawaban dengan menggunakan cara yang berbeda
Contoh Soal dan Penyelesaian
Misalnya, soal nomor 1 di halaman 92 meminta kita untuk menentukan persamaan garis yang melalui titik (2, 3) dan (4, 5). Untuk menyelesaikan soal ini, kita bisa menggunakan rumus gradien:
$$m = \fracy_2 – y_1x_2 – x_1$$
Dengan mengganti nilai yang diketahui, kita dapatkan:
$$m = \frac5 – 34 – 2 = 1$$
Selanjutnya, kita bisa menggunakan rumus persamaan garis:
$$y – y_1 = m(x – x_1)$$
Dengan mengganti nilai yang diketahui, kita dapatkan:
$$y – 3 = 1(x – 2)$$
Bingung sama soal matematika kelas 9 halaman 92? Tenang, banyak kok sumber belajar yang bisa kamu akses. Selain buku pegangan, kamu juga bisa coba cari di internet. Kalau lagi butuh bantuan buat ngerjain soal IPA kelas 9 halaman 159, coba cek kunci jawaban ipa kelas 9 halaman 159 ini.
Semoga membantu, ya! Nah, balik lagi ke soal matematika kelas 9 halaman 92, jangan lupa untuk pahami konsep dasarnya sebelum kamu liat kunci jawaban. Biar belajarnya lebih efektif dan kamu bisa ngerjain soal-soal lain dengan lebih mudah.
$$y – 3 = x – 2$$
$$y = x + 1$$
Jadi, persamaan garis yang melalui titik (2, 3) dan (4, 5) adalah $$y = x + 1$$.
Tips Menghindari Kesalahan
Pastikan kamu memahami konsep dengan baik. Baca soal dengan cermat dan identifikasi informasi yang penting. Periksa kembali jawabanmu dengan menggunakan cara yang berbeda. Jangan lupa untuk menuliskan langkah-langkah penyelesaian dengan jelas dan rapi.
Materi Pendukung
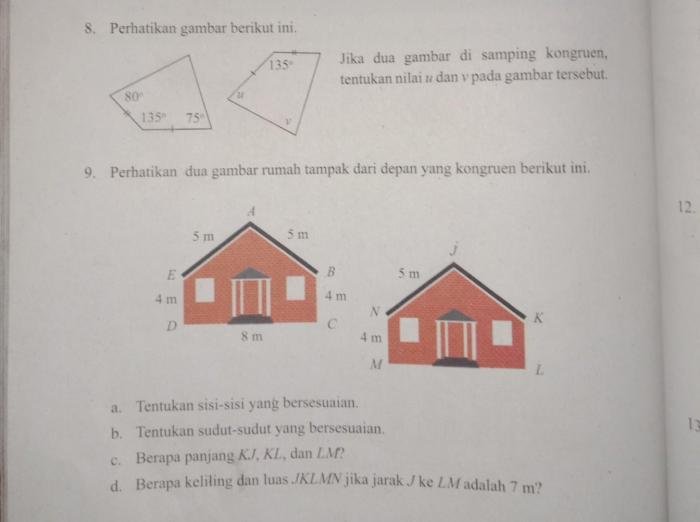
Materi pendukung yang relevan dapat membantu memahami konsep yang diulas di halaman 92. Materi-materi tersebut dapat berupa buku teks, artikel ilmiah, atau sumber daring yang membahas topik serupa. Dengan mempelajari materi pendukung, kamu dapat memperoleh pemahaman yang lebih mendalam dan menyeluruh tentang konsep yang dipelajari.
Daftar Materi Pendukung
Berikut adalah beberapa materi pendukung yang dapat membantu memahami konsep yang diulas di halaman 92:
| Materi Pendukung | Deskripsi Singkat | Contoh Penerapan |
|---|---|---|
| Buku Teks Matematika Kelas 9 | Buku teks matematika kelas 9 umumnya berisi materi yang lengkap dan sistematis tentang konsep-konsep matematika yang dipelajari di kelas 9. | Buku teks matematika kelas 9 dapat digunakan untuk mempelajari materi tentang persamaan linear, persamaan kuadrat, dan sistem persamaan linear. |
| Artikel Ilmiah tentang Matematika | Artikel ilmiah tentang matematika dapat memberikan pemahaman yang lebih mendalam tentang konsep-konsep matematika tertentu. | Artikel ilmiah tentang matematika dapat digunakan untuk mempelajari materi tentang teori bilangan, aljabar linear, atau kalkulus. |
| Sumber Daring tentang Matematika | Sumber daring tentang matematika dapat memberikan akses yang mudah dan cepat ke berbagai materi dan sumber daya matematika. | Sumber daring tentang matematika dapat digunakan untuk mempelajari materi tentang geometri, trigonometri, atau statistika. |
Terakhir

Memahami konsep matematika di halaman 92 tidak hanya penting untuk menyelesaikan soal-soal ujian, tetapi juga untuk mengembangkan kemampuan berpikir kritis dan memecahkan masalah. Dengan mempelajari kunci jawaban dan memahami konsep di baliknya, kamu akan lebih percaya diri dalam menghadapi tantangan matematika di masa depan.
Ingat, belajar matematika adalah proses yang berkelanjutan, jadi jangan ragu untuk bertanya dan berlatih secara konsisten untuk meraih hasil yang maksimal!
Pertanyaan yang Sering Muncul: Kunci Jawaban Matematika Kelas 9 Halaman 92
Apakah kunci jawaban ini cocok untuk semua buku pelajaran matematika kelas 9?
Kunci jawaban ini dirancang untuk membantu memahami konsep matematika yang diulas di halaman 92. Namun, soal dan konsep yang dibahas mungkin sedikit berbeda di setiap buku pelajaran. Pastikan untuk membandingkan dengan buku pelajaranmu.
Bagaimana cara mendapatkan buku pelajaran matematika kelas 9?
Kamu dapat membeli buku pelajaran matematika kelas 9 di toko buku terdekat atau secara online. Pastikan buku tersebut sesuai dengan kurikulum yang berlaku.
Apakah ada cara lain untuk belajar matematika kelas 9 selain menggunakan buku pelajaran?
Ya, ada banyak sumber belajar matematika kelas 9 selain buku pelajaran, seperti video pembelajaran online, situs web edukasi, dan aplikasi belajar interaktif.