Kunci jawaban matematika kelas 8 semester 2 halaman 40 – Bingung dengan soal-soal matematika kelas 8 semester 2 halaman 40? Tenang, kamu tidak sendirian! Banyak siswa yang merasa kesulitan memahami materi dan menyelesaikan soal-soal di halaman tersebut. Artikel ini akan menjadi teman setia kamu dalam menguasai materi pelajaran, memahami konsep, dan menyelesaikan soal-soal dengan mudah.
Yuk, kita bahas bersama!
Materi yang dibahas pada halaman 40 buku matematika kelas 8 semester 2 mencakup konsep penting yang akan membantu kamu memahami berbagai macam soal. Artikel ini akan membahas materi pelajaran secara detail, memberikan contoh soal, dan membahas langkah-langkah penyelesaiannya. Selain itu, kamu juga akan menemukan tips dan trik untuk menghadapi kesulitan dalam memahami materi dan menyelesaikan soal-soal.
Persamaan Linear Dua Variabel: Kunci Jawaban Matematika Kelas 8 Semester 2 Halaman 40

Materi matematika kelas 8 semester 2 halaman 40 membahas tentang persamaan linear dua variabel. Persamaan linear dua variabel merupakan persamaan yang memiliki dua variabel dengan pangkat tertinggi 1. Variabel tersebut biasanya diwakili oleh huruf x dan y.
Pengertian Persamaan Linear Dua Variabel
Persamaan linear dua variabel adalah persamaan yang memiliki dua variabel dengan pangkat tertinggi 1. Variabel tersebut biasanya diwakili oleh huruf x dan y. Persamaan ini dapat ditulis dalam bentuk umum:
ax + by = c
di mana:
- a, b, dan c adalah konstanta (bilangan real)
- x dan y adalah variabel
Contoh persamaan linear dua variabel:
- 2x + 3y = 6
- x – 4y = 10
- 5x + 2y = 1
Solusi Persamaan Linear Dua Variabel
Solusi dari persamaan linear dua variabel adalah pasangan nilai x dan y yang memenuhi persamaan tersebut. Solusi ini dapat direpresentasikan dalam bentuk pasangan terurut (x, y).
Contoh:
Persamaan linear 2x + 3y = 6 memiliki solusi (0, 2) karena:
- 2(0) + 3(2) = 6
- 0 + 6 = 6
- 6 = 6
Persamaan linear ini juga memiliki solusi (3, 0) karena:
- 2(3) + 3(0) = 6
- 6 + 0 = 6
- 6 = 6
Cara Menentukan Solusi Persamaan Linear Dua Variabel
Ada beberapa cara untuk menentukan solusi persamaan linear dua variabel, yaitu:
- Metode Substitusi: Menyelesaikan salah satu variabel dari persamaan pertama dan mensubstitusikan ke persamaan kedua.
- Metode Eliminasi: Mengalikan kedua persamaan dengan konstanta sehingga koefisien salah satu variabel sama, lalu mengurangi kedua persamaan tersebut.
- Metode Grafik: Memplot kedua persamaan pada diagram kartesius. Titik potong kedua garis merupakan solusi dari sistem persamaan tersebut.
Contoh Soal
Tentukan solusi dari sistem persamaan linear berikut:
- x + y = 5
- 2x – y = 1
Penyelesaian:
Kita dapat menggunakan metode eliminasi untuk menyelesaikan soal ini. Dengan menjumlahkan kedua persamaan, kita dapatkan:
- 3x = 6
Kemudian, kita dapat menyelesaikan x:
- x = 6 / 3 = 2
Selanjutnya, kita dapat mensubstitusikan nilai x ke salah satu persamaan untuk mendapatkan nilai y. Misalnya, kita substitusikan x = 2 ke persamaan pertama:
- 2 + y = 5
Kemudian, kita dapat menyelesaikan y:
- y = 5 – 2 = 3
Jadi, solusi dari sistem persamaan linear tersebut adalah (2, 3).
Tabel Ringkasan Materi
| Judul | Penjelasan | Contoh |
|---|---|---|
| Persamaan Linear Dua Variabel | Persamaan yang memiliki dua variabel dengan pangkat tertinggi 1. | 2x + 3y = 6 |
| Solusi Persamaan Linear Dua Variabel | Pasangan nilai x dan y yang memenuhi persamaan. | (0, 2) adalah solusi dari persamaan 2x + 3y = 6. |
| Metode Substitusi | Menyelesaikan salah satu variabel dari persamaan pertama dan mensubstitusikan ke persamaan kedua. | x + y = 5; 2x
Sedang mencari kunci jawaban matematika kelas 8 semester 2 halaman 40? Nah, kalau kamu butuh bantuan untuk mata pelajaran lain, kamu bisa cek kunci jawaban tema 3 kelas 5 halaman 43 yang bisa membantu kamu memahami materi pelajaran. Meskipun berbeda tingkat, memahami konsep dasar dari setiap pelajaran sangat penting untuk membantu kamu dalam belajar. Kembali ke kunci jawaban matematika kelas 8 semester 2 halaman 40, semoga kamu bisa menemukan solusi yang tepat untuk soal-soal yang ada.
|
| Metode Eliminasi | Mengalikan kedua persamaan dengan konstanta sehingga koefisien salah satu variabel sama, lalu mengurangi kedua persamaan tersebut. | x + y = 5; 2xy = 1. Kalikan persamaan pertama dengan 2, kemudian kurangi kedua persamaan. |
| Metode Grafik | Memplot kedua persamaan pada diagram kartesius. Titik potong kedua garis merupakan solusi dari sistem persamaan tersebut. | Gambarlah grafik persamaan x + y = 5 dan 2xy = 1. Titik potong kedua garis tersebut merupakan solusi dari sistem persamaan. |
Latihan Soal
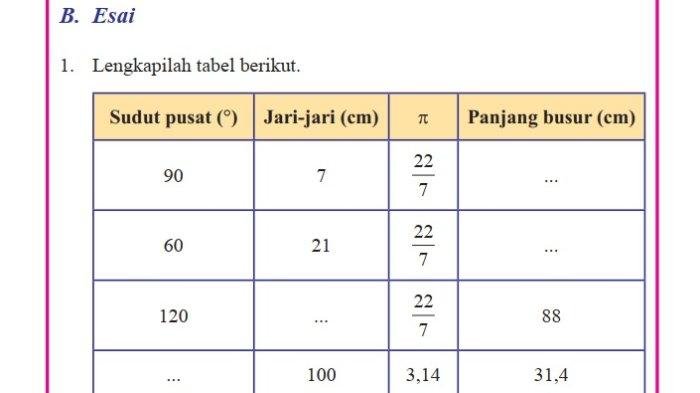
Untuk menguji pemahamanmu tentang materi yang telah dipelajari, berikut adalah beberapa latihan soal yang bisa kamu kerjakan. Soal-soal ini dirancang untuk membantu kamu memahami konsep dan menerapkannya dalam berbagai situasi.
Soal Latihan 1
Soal latihan ini bertujuan untuk menguji pemahamanmu tentang operasi hitung pada bilangan bulat. Kamu akan diminta untuk menyelesaikan operasi penjumlahan, pengurangan, perkalian, dan pembagian pada bilangan bulat positif dan negatif.
- Hitunglah hasil dari (-5) + 7 – 3 x 2.
- Tentukan hasil dari (-12) : (-3) x 4 + 5.
- Selesaikan operasi berikut: 8 – 2 x (5 + 3).
Soal Latihan 2
Soal latihan ini menguji pemahamanmu tentang sifat-sifat operasi hitung pada bilangan bulat. Kamu akan diminta untuk mengidentifikasi sifat-sifat seperti komutatif, asosiatif, dan distributif.
- Jelaskan sifat komutatif pada operasi penjumlahan dan perkalian bilangan bulat.
- Berikan contoh penerapan sifat asosiatif pada operasi penjumlahan dan perkalian bilangan bulat.
- Tunjukkan bagaimana sifat distributif berlaku dalam operasi penjumlahan dan perkalian bilangan bulat.
Soal Latihan 3
Soal latihan ini menguji pemahamanmu tentang operasi hitung pada bilangan pecahan. Kamu akan diminta untuk menyelesaikan operasi penjumlahan, pengurangan, perkalian, dan pembagian pada bilangan pecahan.
- Hitunglah hasil dari 1/2 + 3/4 – 1/8.
- Tentukan hasil dari 2/3 x 5/6 : 1/2.
- Selesaikan operasi berikut: 3/4 – 1/3 + 2/5.
Soal Latihan 4
Soal latihan ini menguji pemahamanmu tentang operasi hitung pada bilangan desimal. Kamu akan diminta untuk menyelesaikan operasi penjumlahan, pengurangan, perkalian, dan pembagian pada bilangan desimal.
- Hitunglah hasil dari 2,5 + 3,75 – 1,25.
- Tentukan hasil dari 4,5 x 2,2 : 1,5.
- Selesaikan operasi berikut: 5,6 – 2,3 x 1,2.
Soal Latihan 5
Soal latihan ini menguji pemahamanmu tentang operasi hitung campuran pada bilangan bulat, pecahan, dan desimal. Kamu akan diminta untuk menyelesaikan operasi yang melibatkan berbagai jenis bilangan.
- Hitunglah hasil dari 2 + 1/2 – 0,5 x 3.
- Tentukan hasil dari 3/4 x (2 + 1/3) – 0,75.
- Selesaikan operasi berikut: (1/2 + 1/4) x 2,5 – 1.
Contoh Soal dan Jawaban
Hitunglah hasil dari (-5) + 7- 3 x 2.
Penyelesaian:
Kita selesaikan operasi perkalian terlebih dahulu, kemudian penjumlahan dan pengurangan.
Cari kunci jawaban matematika kelas 8 semester 2 halaman 40? Tenang, kamu nggak sendirian! Banyak siswa yang juga mencari jawabannya. Meskipun kamu mungkin butuh bantuan untuk memahami materi, jangan lupa untuk tetap berusaha memahami konsepnya ya. Kalau kamu lagi belajar tentang tema 2 kelas 3, kamu bisa cek kunci jawaban tema 2 kelas 3 halaman 4 untuk membantu kamu memahami materi tersebut.
Nah, setelah belajar dari sumber lain, kamu bisa kembali ke soal matematika kelas 8 semester 2 halaman 40 dan coba kerjakan lagi. Ingat, belajar itu proses, dan jangan takut untuk bertanya kalau ada yang nggak dimengerti!
(-5) + 7 – 3 x 2 = (-5) + 7 – 6
= 2 – 6
= -4
Butuh bantuan untuk menyelesaikan soal matematika kelas 8 semester 2 halaman 40? Tenang, banyak sumber yang bisa kamu akses! Tapi kalau kamu lagi cari kunci jawaban pelajaran lain, seperti kunci jawaban pai kelas 7 halaman 48 , kamu bisa coba cari di internet.
Yang penting, jangan lupa untuk memahami konsep dan menyelesaikan soal dengan kemampuanmu sendiri. Setelah itu, kamu bisa cek jawabanmu dengan kunci jawaban matematika kelas 8 semester 2 halaman 40 untuk memastikan pemahamanmu.
Jadi, hasil dari (-5) + 7 – 3 x 2 adalah -4.
Penerapan Konsep

Konsep yang dipelajari pada halaman 40, seperti persamaan linear, memiliki aplikasi luas dalam kehidupan sehari-hari. Persamaan linear membantu kita memahami dan menyelesaikan berbagai masalah, mulai dari perencanaan keuangan hingga menentukan jarak tempuh kendaraan.
Contoh Penerapan Konsep
Misalnya, dalam perencanaan keuangan, kita dapat menggunakan persamaan linear untuk menghitung total biaya yang harus dikeluarkan untuk membeli barang tertentu. Jika kita tahu harga per unit barang dan jumlah unit yang ingin dibeli, kita dapat menggunakan persamaan linear untuk menentukan total biaya.
Sebagai contoh, jika harga satu kilogram beras adalah Rp10.000 dan kita ingin membeli 5 kilogram beras, kita dapat menggunakan persamaan linear berikut untuk menghitung total biaya:
Total biaya = Harga per kilogram x Jumlah kilogram
Total biaya = Rp10.000 x 5
Total biaya = Rp50.000
Dari persamaan ini, kita dapat mengetahui bahwa total biaya yang harus dikeluarkan untuk membeli 5 kilogram beras adalah Rp50.000.
Poin Penting Penerapan Konsep
- Persamaan linear dapat membantu kita dalam memecahkan masalah yang melibatkan hubungan linear antara dua variabel.
- Konsep ini dapat diterapkan dalam berbagai bidang, seperti ekonomi, ilmu pengetahuan, dan teknologi.
- Dengan memahami persamaan linear, kita dapat membuat keputusan yang lebih tepat dan efektif dalam kehidupan sehari-hari.
Kesulitan dan Solusi

Materi matematika kelas 8 semester 2 halaman 40 mungkin terasa menantang bagi sebagian siswa. Ada beberapa konsep yang memerlukan pemahaman mendalam dan latihan yang cukup untuk menguasainya. Artikel ini akan mengidentifikasi beberapa kesulitan yang mungkin dihadapi siswa dan memberikan solusi yang dapat membantu mereka memahami materi dengan lebih baik.
Memahami Konsep Persamaan Linear Dua Variabel, Kunci jawaban matematika kelas 8 semester 2 halaman 40
Persamaan linear dua variabel merupakan konsep dasar yang penting dalam aljabar. Kesulitan yang sering dihadapi siswa adalah memahami konsep ini secara utuh, terutama dalam menentukan solusi dan menggambar grafiknya.
- Kesulitan:Siswa mungkin kesulitan memahami bahwa solusi dari persamaan linear dua variabel adalah pasangan terurut (x, y) yang memenuhi persamaan tersebut.
- Solusi:Gunakan contoh konkret dan ilustrasi untuk menjelaskan konsep ini. Misalnya, tunjukkan bagaimana pasangan terurut (2, 3) merupakan solusi dari persamaan 2x + y = 7.
- Kesulitan:Siswa mungkin kesulitan menggambar grafik persamaan linear dua variabel.
- Solusi:Gunakan tabel untuk menentukan beberapa titik yang memenuhi persamaan dan kemudian plot titik-titik tersebut pada bidang koordinat. Hubungkan titik-titik tersebut dengan garis lurus.
Menerapkan Metode Substitusi dan Eliminasi
Metode substitusi dan eliminasi adalah dua metode penting untuk menyelesaikan sistem persamaan linear dua variabel. Kesulitan yang sering dihadapi siswa adalah dalam memilih metode yang tepat dan dalam menerapkan langkah-langkah metode tersebut.
- Kesulitan:Siswa mungkin kesulitan dalam memilih metode yang tepat untuk menyelesaikan sistem persamaan linear dua variabel.
- Solusi:Jelaskan bahwa metode substitusi lebih efektif jika salah satu persamaan sudah memiliki variabel yang terisolasi. Metode eliminasi lebih efektif jika koefisien dari salah satu variabel dalam kedua persamaan memiliki tanda yang berlawanan atau merupakan kelipatan satu sama lain.
- Kesulitan:Siswa mungkin kesulitan dalam menerapkan langkah-langkah metode substitusi dan eliminasi.
- Solusi:Gunakan contoh soal yang mudah dipahami dan tunjukkan langkah-langkah secara detail. Jelaskan mengapa setiap langkah dilakukan dan bagaimana langkah tersebut membantu menyelesaikan sistem persamaan.
Menyelesaikan Masalah Kontekstual
Salah satu kesulitan yang sering dihadapi siswa adalah dalam menyelesaikan masalah kontekstual yang melibatkan persamaan linear dua variabel. Siswa mungkin kesulitan dalam menerjemahkan masalah kontekstual ke dalam sistem persamaan linear.
- Kesulitan:Siswa mungkin kesulitan dalam memahami bagaimana masalah kontekstual dapat diubah menjadi sistem persamaan linear dua variabel.
- Solusi:Gunakan contoh soal yang realistis dan pandu siswa dalam menentukan variabel yang tepat dan dalam menuliskan persamaan yang mewakili masalah tersebut.
- Kesulitan:Siswa mungkin kesulitan dalam menginterpretasikan solusi dari sistem persamaan dalam konteks masalah.
- Solusi:Setelah menyelesaikan sistem persamaan, mintalah siswa untuk menginterpretasikan solusi dalam konteks masalah. Misalnya, jika solusi adalah (5, 10), apa artinya solusi tersebut dalam konteks masalah?
Kesimpulan Akhir

Dengan memahami konsep dan latihan yang cukup, kamu pasti dapat menguasai materi matematika kelas 8 semester 2 halaman 40. Jangan ragu untuk mempelajari materi ini secara berulang dan bertanya jika kamu mengalami kesulitan. Ingat, belajar matematika itu menyenangkan dan bermanfaat untuk kehidupan sehari-hari.
Selamat belajar!
FAQ Terkini
Apakah materi di halaman 40 sulit?
Tidak semua orang merasa sulit. Dengan latihan dan pemahaman yang baik, materi ini bisa dipelajari dengan mudah.
Bagaimana cara mendapatkan nilai bagus di matematika?
Rajin belajar, memahami konsep, dan berlatih soal secara rutin adalah kunci untuk mendapatkan nilai bagus.
Apa saja yang harus dipelajari di kelas 8 semester 2?
Materi kelas 8 semester 2 mencakup berbagai topik seperti persamaan linear, persamaan kuadrat, bangun ruang, dan lainnya.