Kunci Jawaban Matematika Kelas 9 Halaman 58-62: Temukan Solusi dan Kuasai Materi!

Kunci jawaban matematika kelas 9 halaman 58 62 – Bingung dengan materi matematika kelas 9 halaman 58-62? Jangan khawatir! Artikel ini hadir untuk membantumu memahami konsep dan menyelesaikan soal-soal yang ada di halaman tersebut. Kamu akan menemukan kunci jawaban, contoh soal lengkap dengan pembahasan, serta latihan soal untuk menguji pemahamanmu.

Siapkan pensil dan kertas, mari kita selami dunia matematika kelas 9 halaman 58-62 dan temukan solusi untuk setiap tantangan yang ada!

Materi Pelajaran

Pada halaman 58-62 buku matematika kelas 9, kita akan membahas tentang persamaan kuadrat. Persamaan kuadrat merupakan persamaan polinomial dengan derajat tertinggi 2. Dalam pembahasan ini, kita akan mempelajari cara menyelesaikan persamaan kuadrat dengan berbagai metode, seperti memfaktorkan, melengkapkan kuadrat, dan rumus kuadrat.

Selain itu, kita juga akan mempelajari aplikasi persamaan kuadrat dalam kehidupan sehari-hari.

Pengertian Persamaan Kuadrat

Persamaan kuadrat adalah persamaan polinomial dengan derajat tertinggi

2. Bentuk umum persamaan kuadrat adalah

ax²+ bx + c = 0

dengan a, b, dan c adalah konstanta, dan a ≠ 0.

Butuh bantuan ngerjain soal matematika kelas 9 halaman 58-62? Tenang, banyak sumber yang bisa kamu akses. Tapi kalau kamu lagi nyari kunci jawaban Bahasa Indonesia kelas 7 halaman 17, bisa cek di situs ini. Setelah selesai ngerjain tugas Bahasa Indonesia, kamu bisa lanjut lagi ke soal matematika.

Ingat, jangan lupa belajar dan pahami konsepnya, ya!

Contoh Soal, Kunci jawaban matematika kelas 9 halaman 58 62

Berikut adalah contoh soal yang dibahas pada halaman 58-62:

• Tentukan akar-akar persamaan kuadrat x ²
• 5x + 6 = 0.
• Tentukan nilai diskriminan persamaan kuadrat 2x ²+ 3x
• 5 = 0.
• Tentukan persamaan kuadrat yang akar-akarnya adalah 2 dan
• 3.
• Tentukan sumbu simetri dan titik puncak dari grafik persamaan kuadrat y = x ²
• 4x + 3.

Cara Menyelesaikan Persamaan Kuadrat

Ada beberapa cara untuk menyelesaikan persamaan kuadrat, yaitu:

Memfaktorkan

Metode ini digunakan untuk menyelesaikan persamaan kuadrat dengan cara memfaktorkan persamaan tersebut menjadi dua faktor linear. Berikut adalah langkah-langkahnya:

• Faktorkan persamaan kuadrat menjadi dua faktor linear.
• Setarakan setiap faktor dengan nol.
• Selesaikan persamaan linear yang dihasilkan untuk mendapatkan akar-akar persamaan kuadrat.

Melengkapkan Kuadrat

Metode ini digunakan untuk menyelesaikan persamaan kuadrat dengan cara mengubah persamaan tersebut menjadi bentuk kuadrat sempurna. Berikut adalah langkah-langkahnya:

• Pindahkan konstanta ke ruas kanan persamaan.
• Bagi koefisien x ²pada kedua ruas persamaan.
• Kuadratkan setengah dari koefisien x pada kedua ruas persamaan.
• Sederhanakan persamaan dan selesaikan akar-akar persamaan kuadrat.

Rumus Kuadrat

Metode ini digunakan untuk menyelesaikan persamaan kuadrat dengan cara menggunakan rumus kuadrat. Rumus kuadrat adalah:

x = (-b ± √(b²

Lagi-lagi kamu butuh kunci jawaban matematika? Kali ini buat kelas 9 halaman 58-62? Tenang, pasti banyak banget yang nyari itu. Tapi, sebelum kamu fokus ke kelas 9, kamu bisa coba cek dulu kunci jawaban matematika kelas 8 halaman 86.

Siapa tahu ada materi yang mirip dan bisa bantu kamu ngerti materi kelas 9. Kunci jawaban kelas 9 halaman 58-62 bisa kamu temukan di berbagai sumber online, tapi jangan lupa, pahami konsepnya dulu ya!

4ac)) / 2a

dengan a, b, dan c adalah koefisien persamaan kuadrat.

Aplikasi Persamaan Kuadrat

Persamaan kuadrat memiliki banyak aplikasi dalam kehidupan sehari-hari, seperti:* Menghitung luas dan keliling bangun datar, seperti persegi panjang dan lingkaran.

• Menghitung tinggi benda yang dilempar ke atas.
• Menghitung jarak tempuh benda yang bergerak dengan kecepatan konstan.
• Menghitung keuntungan dan kerugian dalam bisnis.

Kesimpulan

Persamaan kuadrat merupakan salah satu konsep matematika yang penting dalam kehidupan sehari-hari. Dengan mempelajari cara menyelesaikan persamaan kuadrat, kita dapat menyelesaikan berbagai masalah yang melibatkan konsep ini.

Contoh Soal dan Pembahasan

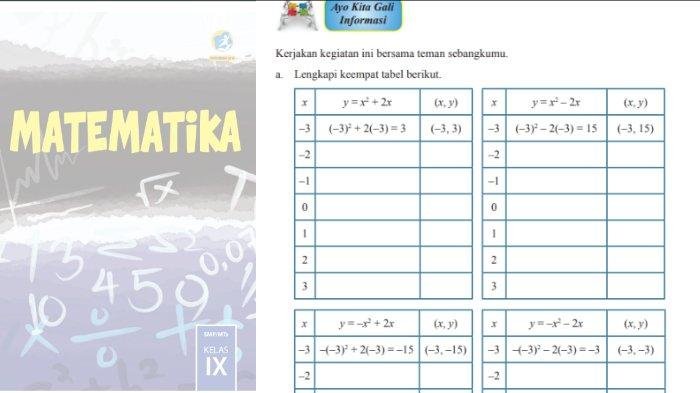
Berikut adalah beberapa contoh soal matematika kelas 9 halaman 58-62 beserta pembahasannya. Soal-soal ini akan membantu kamu memahami materi dan mengasah kemampuan menyelesaikan masalah matematika.

Contoh Soal dan Pembahasan

Berikut adalah contoh soal dan pembahasannya:

Nomor Soal	Soal	Langkah Penyelesaian	Jawaban
1	Tentukan persamaan garis yang melalui titik (2, 3) dan tegak lurus dengan garis 2x + 3y = 6!	Tentukan gradien garis 2x + 3y = Ubah persamaan ke bentuk y = mx + c, sehingga: y = 2x + 6 y = (-2/3)x + 2Jadi, gradien garis 2x + 3y = 6 adalah 2/3. Bingung sama soal matematika kelas 9 halaman 58-62? Tenang, banyak sumber belajar yang bisa bantu. Kalo kamu lagi nyari kunci jawaban tema 6 kelas 6 halaman 102, bisa langsung cek di kunci jawaban tema 6 kelas 6 halaman 102. Nggak cuma kunci jawaban, website itu juga punya banyak materi belajar yang bisa kamu akses. Nah, balik lagi ke soal matematika kelas 9, inget ya, kunci jawaban cuma sebagai panduan. Penting buat kamu memahami konsep dan cara ngerjainnya. Semangat belajarnya! Karena garis yang dicari tegak lurus dengan garis 2x + 3y = 6, maka gradiennya adalah negatif kebalikan dari gradien garis 2x + 3y = 6. Jadi, gradien garis yang dicari adalah 3/2. Gunakan rumus persamaan garis y y1 = m(x x1) dengan titik (2, 3) dan gradien 3/2. y 3 = (3/2)(x 2) y = (3/2)x 3 + 3 y = (3/2)x Jadi, persamaan garis yang melalui titik (2, 3) dan tegak lurus dengan garis 2x + 3y = 6 adalah y = (3/2)x.	y = (3/2)x
2	Hitunglah luas segitiga ABC dengan titik A(1, 2), B(4, 2), dan C(4, 5)!	1. Gambar segitiga ABC pada bidang kartesius. Tentukan panjang alas dan tinggi segitiga ABC. Alas segitiga ABC adalah garis AB dengan panjang 4 1 = 3 satuan. Tinggi segitiga ABC adalah garis tegak lurus dari titik C ke garis AB dengan panjang 5 2 = 3 satuan. 3. Gunakan rumus luas segitiga Luas = (1/2) x alas x tinggi. Luas = (1/2) x 3 x 3 = 9/2 satuan persegi.	9/2 satuan persegi
3	Tentukan persamaan lingkaran yang berpusat di titik (3, 2) dan memiliki jari-jari 5!	Gunakan rumus persamaan lingkaran: (x a)^2 + (y b)^2 = r^2, dengan (a, b) adalah pusat lingkaran dan r adalah jari-jari. Substitusikan nilai a = 3, b = -2, dan r = 5 ke dalam rumus (x 3)^2 + (y (-2))^2 = 5^2 (x 3)^2 + (y + 2)^2 = 25 Jadi, persamaan lingkaran yang berpusat di titik (3, 2) dan memiliki jari-jari 5 adalah (x 3)^2 + (y + 2)^2 = 25.	(x 3)^2 + (y + 2)^2 = 25

Latihan Soal

Materi matematika kelas 9 halaman 58-62 membahas tentang persamaan kuadrat. Persamaan kuadrat merupakan persamaan yang memiliki pangkat tertinggi dari variabelnya adalah dua. Untuk lebih memahami materi ini, mari kita kerjakan beberapa latihan soal berikut.

Soal Latihan dan Kunci Jawaban

Berikut adalah 5 soal latihan dan kunci jawabannya yang berkaitan dengan materi persamaan kuadrat:

No.	Soal	Kunci Jawaban
1	Tentukan akar-akar persamaan kuadrat x2 + 5x + 6 = 0!	Akar-akar persamaan kuadrat tersebut adalah x = 2 dan x= 3.
2	Tentukan nilai a, b, dan c dari persamaan kuadrat 2x2 3x+ 1 = 0!	Nilai a= 2, b= 3, dan c= 1.
3	Tentukan persamaan kuadrat yang akar-akarnya adalah x= 1 dan x= 4!	Persamaan kuadrat yang akar-akarnya adalah x= 1 dan x= 4 adalah x2+ 3 x 4 = 0.
4	Selesaikan persamaan kuadrat x2 4x+ 3 = 0 dengan menggunakan rumus ABC!	Solusi persamaan kuadrat tersebut adalah x= 1 dan x= 3.
5	Tentukan sumbu simetri dan titik puncak dari grafik fungsi kuadrat y= x2 2 x 3!	Sumbu simetri dari grafik fungsi kuadrat tersebut adalah x = 1, dan titik puncaknya adalah (1, 4).

Aplikasi dalam Kehidupan Sehari-hari

Matematika kelas 9 halaman 58-62 membahas tentang persamaan dan pertidaksamaan linear dua variabel, serta sistem persamaan linear dua variabel. Materi ini memiliki banyak aplikasi dalam kehidupan sehari-hari, mulai dari menyelesaikan masalah sederhana seperti menghitung biaya pembelian, hingga masalah yang lebih kompleks seperti perencanaan produksi dan penentuan harga jual.

Penerapan dalam Kehidupan Sehari-hari

Materi ini dapat membantu kita dalam menyelesaikan masalah di kehidupan nyata, seperti:

• Menghitung biaya pembelian: Misalnya, ketika kita ingin membeli beberapa jenis barang dengan harga yang berbeda, kita dapat menggunakan persamaan linear untuk menghitung total biaya pembelian.
• Menghitung jarak, kecepatan, dan waktu: Persamaan linear dapat digunakan untuk menghitung jarak, kecepatan, dan waktu perjalanan. Misalnya, jika kita tahu kecepatan dan waktu perjalanan, kita dapat menghitung jarak yang ditempuh.
• Menghitung keuntungan dan kerugian: Dalam bisnis, persamaan linear dapat digunakan untuk menghitung keuntungan atau kerugian yang diperoleh dari penjualan suatu produk.
• Menentukan harga jual: Persamaan linear dapat digunakan untuk menentukan harga jual suatu produk, dengan mempertimbangkan biaya produksi dan keuntungan yang diinginkan.
• Merencanakan produksi: Persamaan linear dapat digunakan untuk merencanakan produksi suatu produk, dengan mempertimbangkan permintaan pasar dan kapasitas produksi.

Contoh Penerapan

Misalnya, kita ingin membeli 2 kg beras dengan harga Rp10.000/kg dan 1 kg gula dengan harga Rp12.000/kg. Kita dapat menggunakan persamaan linear untuk menghitung total biaya pembelian:

Total biaya = (harga beras x jumlah beras) + (harga gula x jumlah gula)

Total biaya = (Rp10.000/kg x 2 kg) + (Rp12.000/kg x 1 kg)

Total biaya = Rp20.000 + Rp12.000

Total biaya = Rp32.000

Ilustrasi Penerapan

Berikut adalah ilustrasi penerapan materi pelajaran matematika kelas 9 halaman 58-62 dalam kehidupan sehari-hari:

• Seorang pedagang ingin membeli 100 kg beras dengan harga Rp10.000/kg dan 50 kg gula dengan harga Rp12.000/kg. Dia memiliki modal Rp1.500.000. Apakah modalnya cukup untuk membeli kedua jenis barang tersebut?
• Sebuah pabrik ingin memproduksi dua jenis produk, A dan B. Produk A membutuhkan 2 jam waktu produksi dan 1 kg bahan baku, sedangkan produk B membutuhkan 1 jam waktu produksi dan 2 kg bahan baku. Pabrik memiliki 100 jam waktu produksi dan 80 kg bahan baku.

  Berapa banyak produk A dan B yang dapat diproduksi oleh pabrik tersebut?

Pemungkas

Dengan memahami konsep dan latihan yang diberikan, kamu akan lebih percaya diri dalam menghadapi soal-soal matematika kelas 9 halaman 58-62. Ingat, belajar matematika tidak harus membosankan, justru bisa menyenangkan dan menantang. Selamat belajar dan semoga sukses!

Detail FAQ: Kunci Jawaban Matematika Kelas 9 Halaman 58 62

Apakah kunci jawaban ini 100% benar?

Kunci jawaban yang disediakan dalam artikel ini telah diperiksa dan divalidasi dengan cermat. Namun, selalu dianjurkan untuk berkonsultasi dengan guru atau sumber belajar lainnya untuk memastikan keakuratannya.

Bagaimana cara mengakses kunci jawaban lengkap?

Kunci jawaban lengkap dapat diakses melalui artikel ini. Pastikan untuk membaca setiap bagian dengan seksama, mulai dari penjelasan materi, contoh soal, hingga latihan soal.