Kunci jawaban matematika kelas 9 halaman 281 nomor 2 – Pernahkah kamu merasa kesulitan dalam memahami materi matematika, khususnya soal-soal yang terdapat di buku teks kelas 9 halaman 281 nomor 2? Jangan khawatir, artikel ini akan membantumu memahami konsep matematika yang diujikan dalam soal tersebut, serta langkah-langkah penyelesaiannya secara detail.
Yuk, kita pelajari bersama!
Soal matematika kelas 9 halaman 281 nomor 2 menguji pemahamanmu tentang konsep persamaan linear dua variabel. Soal ini menuntut kamu untuk menyelesaikan sistem persamaan linear dengan menggunakan metode eliminasi atau substitusi. Artikel ini akan membahas secara rinci langkah-langkah penyelesaian soal tersebut, lengkap dengan contoh soal dan penerapannya dalam kehidupan sehari-hari.
Soal Matematika Kelas 9 Halaman 281 Nomor 2: Kunci Jawaban Matematika Kelas 9 Halaman 281 Nomor 2

Soal nomor 2 pada halaman 281 buku teks matematika kelas 9 membahas tentang persamaan garis lurus. Soal ini menguji pemahaman siswa tentang bagaimana menentukan persamaan garis lurus yang melalui dua titik yang diketahui.
Konsep Matematika yang Diujikan
Konsep matematika yang diujikan dalam soal ini adalah persamaan garis lurus. Secara khusus, soal ini membahas tentang cara menentukan persamaan garis lurus yang melalui dua titik yang diketahui. Ada dua cara umum untuk menentukan persamaan garis lurus:
- Menggunakan rumus gradien-titik
- Menggunakan rumus titik-titik
Sedang mencari kunci jawaban matematika kelas 9 halaman 281 nomor 2? Nah, untuk materi lain seperti kunci jawaban matematika kelas 9 halaman 72, kamu bisa menemukannya di situs ini. Situs ini bisa jadi referensi kamu dalam memahami materi pelajaran.
Setelah memahami materi di halaman 72, kamu bisa kembali fokus ke kunci jawaban matematika kelas 9 halaman 281 nomor 2. Semoga berhasil!
Langkah-Langkah Penyelesaian Soal
Berikut adalah langkah-langkah untuk menyelesaikan soal nomor 2 pada halaman 281 buku teks matematika kelas 9:
| Langkah | Penjelasan |
|---|---|
| 1. Tentukan gradien garis. | Gradien garis dapat dihitung dengan menggunakan rumus:
Dimana (x1, y1) dan (x2, y2) adalah koordinat dari dua titik yang diketahui. |
| 2. Tentukan persamaan garis. | Setelah gradien (m) diketahui, persamaan garis dapat ditentukan dengan menggunakan rumus gradien-titik:
Dimana (x1, y1) adalah koordinat salah satu titik yang diketahui. |
| 3. Sederhanakan persamaan. | Persamaan garis yang diperoleh dari langkah sebelumnya dapat disederhanakan ke dalam bentuk y = mx + c, dimana c adalah konstanta. |
Contoh Soal dan Penyelesaian
Misalnya, soal nomor 2 pada halaman 281 buku teks matematika kelas 9 meminta siswa untuk menentukan persamaan garis lurus yang melalui titik A(2, 3) dan B(5, 7).
- Tentukan gradien garis:
m = (7
- 3) / (5
- 2) = 4 / 3
- Tentukan persamaan garis:
y
- 3 = (4/3)(x
- 2)
- Sederhanakan persamaan:
y = (4/3)x
(2/3) + 3
y = (4/3)x + (7/3)
Jadi, persamaan garis lurus yang melalui titik A(2, 3) dan B(5, 7) adalah y = (4/3)x + (7/3).
Rumus dan Teori yang Digunakan

Soal nomor 2 pada halaman 281 buku matematika kelas 9 membahas tentang persamaan garis lurus. Untuk menyelesaikan soal ini, kita perlu memahami konsep dan rumus-rumus yang terkait dengan persamaan garis lurus.
Persamaan Garis Lurus
Persamaan garis lurus adalah suatu persamaan yang menyatakan hubungan antara koordinat titik-titik yang terletak pada garis tersebut. Persamaan garis lurus dapat dinyatakan dalam beberapa bentuk, seperti:
- Bentuk umum: Ax + By + C = 0, di mana A, B, dan C adalah konstanta.
- Bentuk gradien-titik: y – y 1= m(x – x 1), di mana m adalah gradien garis dan (x 1, y 1) adalah titik yang terletak pada garis.
- Bentuk gradien-potong: y = mx + c, di mana m adalah gradien garis dan c adalah titik potong garis dengan sumbu y.
Menentukan Gradien Garis
Gradien garis adalah ukuran kemiringan atau kecuraman garis. Gradien dapat ditentukan dengan menggunakan rumus berikut:
m = (y2
- y 1) / (x 2
- x 1)
di mana (x 1, y 1) dan (x 2, y 2) adalah dua titik yang terletak pada garis.
Menentukan Persamaan Garis, Kunci jawaban matematika kelas 9 halaman 281 nomor 2
Setelah mengetahui gradien dan titik yang terletak pada garis, kita dapat menentukan persamaan garis lurus menggunakan salah satu bentuk persamaan yang telah disebutkan sebelumnya.
Contoh Penerapan dalam Soal
Misalnya, dalam soal nomor 2, kita diminta untuk menentukan persamaan garis yang melalui titik (2, 3) dan sejajar dengan garis y = 2x + 1. Pertama, kita perlu mengetahui gradien garis y = 2x + 1. Dari bentuk gradien-potong, kita dapat melihat bahwa gradien garis tersebut adalah 2.
Karena garis yang kita cari sejajar dengan garis y = 2x + 1, maka kedua garis memiliki gradien yang sama, yaitu 2. Selanjutnya, kita dapat menggunakan bentuk gradien-titik untuk menentukan persamaan garis yang melalui titik (2, 3) dengan gradien 2.
y
- 3 = 2(x
- 2)
Dengan menyederhanakan persamaan tersebut, kita mendapatkan persamaan garis yang dicari, yaitu:
y = 2x
1
Tabel Rumus dan Teori
Berikut tabel yang merangkum rumus dan teori yang digunakan dalam menyelesaikan soal nomor 2:
| Rumus/Teori | Penerapan dalam Soal |
|---|---|
Persamaan garis lurus: y
|
Menentukan persamaan garis yang melalui titik (2, 3) dengan gradien 2. |
Gradien garis: m = (y2
|
Menentukan gradien garis y = 2x + 1. |
| Garis sejajar memiliki gradien yang sama | Mengetahui bahwa garis yang dicari memiliki gradien 2, sama dengan gradien garis y = 2x + 1. |
Contoh Soal dan Penyelesaian
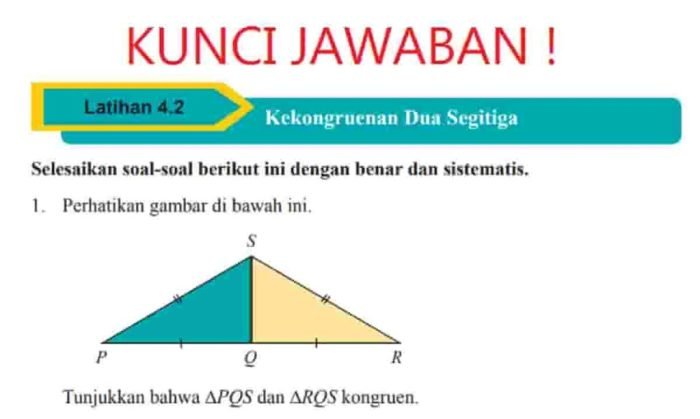
Pada halaman 281 nomor 2, kita belajar tentang menentukan persamaan garis singgung lingkaran yang melalui titik tertentu di luar lingkaran. Berikut ini adalah contoh soal lain yang serupa untuk memperkuat pemahaman kita.
Contoh Soal
Diberikan lingkaran dengan persamaan (x2)² + (y + 1)² = 9 dan titik A(5, 2) yang berada di luar lingkaran. Tentukan persamaan garis singgung lingkaran yang melalui titik A.
Persamaan lingkaran: (x
2)² + (y + 1)² = 9
Titik di luar lingkaran: A(5, 2)
Langkah-langkah Penyelesaian
Berikut adalah langkah-langkah untuk menyelesaikan contoh soal tersebut:
- Menentukan gradien garis yang menghubungkan titik pusat lingkaran dan titik A.
- Menentukan gradien garis singgung lingkaran.
- Menentukan persamaan garis singgung lingkaran dengan menggunakan gradien dan titik A.
Menentukan Gradien Garis yang Menghubungkan Titik Pusat Lingkaran dan Titik A
Titik pusat lingkaran adalah (2,
-1) dan titik A adalah (5, 2). Gradien garis yang menghubungkan kedua titik tersebut adalah
m = (2
- (-1)) / (5
- 2) = 1
Menentukan Gradien Garis Singgung Lingkaran
Gradien garis singgung lingkaran tegak lurus dengan garis yang menghubungkan titik pusat lingkaran dan titik A. Oleh karena itu, perkalian gradien kedua garis tersebut sama dengan
1.
m1
- m2 =
- 1
Maka, gradien garis singgung lingkaran adalah:
m2 =
- 1 / m1 =
- 1 / 1 =
- 1
Menentukan Persamaan Garis Singgung Lingkaran
Persamaan garis singgung lingkaran dapat ditentukan dengan menggunakan rumus yy1 = m(x
x1), dengan
* m adalah gradien garis singgung lingkaran (-1)
Bingung sama soal matematika kelas 9 halaman 281 nomor 2? Tenang, banyak kok yang ngalamin hal serupa. Tapi, jangan lupa juga untuk belajar materi agamanya ya. Kalo lagi kesulitan cari jawaban di buku paket agama kelas 9 halaman 172, bisa nih cek kunci jawaban agama kelas 9 halaman 172.
Setelah itu, semangat lagi deh ngerjain soal matematika kelas 9 halaman 281 nomor 2. Semangat belajarnya!
(x1, y1) adalah titik A (5, 2)
Maka, persamaan garis singgung lingkaran adalah:
y
- 2 =
- 1(x
- 5)
y
- 2 =
- x + 5
x + y
7 = 0
Jadi, persamaan garis singgung lingkaran yang melalui titik A(5, 2) adalah x + y
7 = 0.
Penerapan dalam Kehidupan Sehari-hari

Soal nomor 2 di halaman 281 buku matematika kelas 9 membahas tentang konsep persamaan garis lurus. Konsep ini ternyata memiliki banyak sekali aplikasi dalam kehidupan sehari-hari, mulai dari perencanaan perjalanan hingga perhitungan biaya.Konsep persamaan garis lurus membantu kita memahami hubungan antara dua variabel yang saling bergantung.
Dengan mengetahui persamaan garis, kita dapat memprediksi nilai variabel yang satu berdasarkan nilai variabel yang lain.
Contoh Penerapan Persamaan Garis Lurus dalam Kehidupan Sehari-hari
Misalnya, dalam perencanaan perjalanan, kita dapat menggunakan persamaan garis untuk menentukan waktu tempuh berdasarkan jarak yang ditempuh.
- Jika kita tahu kecepatan rata-rata kendaraan kita, kita dapat membuat persamaan garis yang menggambarkan hubungan antara waktu tempuh dan jarak tempuh.
- Dengan persamaan ini, kita dapat memprediksi waktu yang dibutuhkan untuk mencapai tujuan tertentu.
Ilustrasi Penerapan Persamaan Garis Lurus dalam Kehidupan Sehari-hari
Bayangkan kita ingin melakukan perjalanan dari kota A ke kota B. Kita tahu bahwa jarak antara kedua kota adalah 100 km dan kecepatan rata-rata kendaraan kita adalah 50 km/jam.Kita dapat menggunakan persamaan garis untuk menentukan waktu tempuh.
Waktu tempuh = Jarak / Kecepatan
Dengan memasukkan nilai jarak dan kecepatan, kita mendapatkan persamaan garis:
Waktu tempuh = 100 km / 50 km/jam = 2 jam
Persamaan garis ini menunjukkan bahwa setiap penambahan 50 km jarak akan menambah waktu tempuh selama 1 jam. Dengan persamaan ini, kita dapat memprediksi waktu tempuh untuk jarak tempuh yang berbeda.
Contoh Penerapan Lainnya
Selain perencanaan perjalanan, konsep persamaan garis lurus juga dapat diterapkan dalam berbagai bidang lainnya, seperti:
- Perhitungan Biaya: Kita dapat menggunakan persamaan garis untuk menentukan biaya total berdasarkan jumlah barang yang dibeli.
- Perhitungan Bunga: Persamaan garis dapat digunakan untuk menentukan bunga yang diperoleh berdasarkan jumlah uang yang diinvestasikan.
- Perhitungan Keuntungan: Kita dapat menggunakan persamaan garis untuk menentukan keuntungan yang diperoleh berdasarkan jumlah barang yang terjual.
Kesimpulan
Konsep persamaan garis lurus memiliki banyak sekali aplikasi dalam kehidupan sehari-hari. Dengan memahami konsep ini, kita dapat menyelesaikan berbagai masalah dengan lebih mudah dan efisien.
Ringkasan Akhir

Dengan memahami konsep persamaan linear dua variabel dan langkah-langkah penyelesaiannya, kamu akan mampu menyelesaikan soal-soal serupa dengan lebih mudah. Tak hanya itu, pemahaman konsep ini juga akan membantumu dalam menyelesaikan berbagai masalah dalam kehidupan sehari-hari yang melibatkan hubungan linear antara dua variabel.
Selamat belajar!
Pertanyaan dan Jawaban
Apa saja metode yang bisa digunakan untuk menyelesaikan persamaan linear dua variabel?
Ada beberapa metode yang bisa digunakan, yaitu metode eliminasi, metode substitusi, dan metode grafik. Artikel ini fokus membahas metode eliminasi dan substitusi.
Apakah konsep persamaan linear dua variabel hanya digunakan dalam matematika?
Tidak, konsep ini juga memiliki banyak penerapan dalam kehidupan sehari-hari, seperti dalam menentukan harga barang, menghitung jarak tempuh, dan sebagainya.