Kunci jawaban matematika kelas 9 halaman 264 – Bingung dengan soal-soal matematika di halaman 264 buku kelas 9? Tenang, artikel ini akan membantumu memahami konsep dan langkah-langkah untuk menyelesaikannya. Kita akan membahas materi yang dibahas, contoh soal, rumus yang relevan, dan langkah-langkah detail dalam menyelesaikannya.
Tak hanya itu, kita juga akan membahas pentingnya memahami konsep dasar matematika dalam menyelesaikan soal-soal yang kompleks. Artikel ini juga dilengkapi dengan latihan soal dan pembahasan lengkap untuk mengasah kemampuanmu. Siap untuk menguasai materi matematika kelas 9 halaman 264?
Mengenal Soal Matematika Kelas 9 Halaman 264
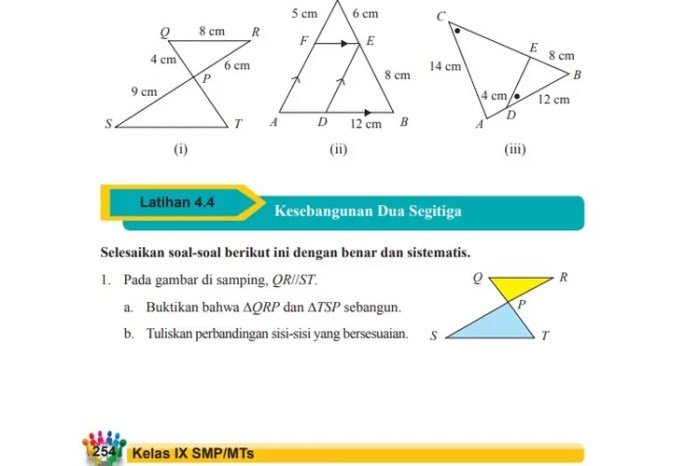
Halaman 264 pada buku matematika kelas 9 umumnya berisi soal-soal yang berkaitan dengan materi tertentu. Materi yang dibahas bisa bervariasi, tergantung pada kurikulum dan buku teks yang digunakan.
Materi yang Dibahas
Untuk mengetahui materi yang dibahas pada halaman 264, kamu perlu melihat buku teks matematika kelas 9 yang kamu gunakan. Materi yang mungkin dibahas bisa meliputi:
- Persamaan dan Pertidaksamaan Linear
- Sistem Persamaan Linear Dua Variabel
- Fungsi Linear
- Persamaan Garis Lurus
- Gradien Garis
- Persamaan Kuadrat
- Fungsi Kuadrat
- Sistem Persamaan Kuadrat
- Bangun Datar
- Bangun Ruang
- Statistika
- Peluang
Contoh Soal dan Jenis Soal
Berikut adalah contoh soal yang mungkin terdapat pada halaman 264, beserta jenis soalnya:
Tentukan himpunan penyelesaian dari sistem persamaan linear dua variabel berikut:
2x + 3y = 7
x- y = 1
Butuh bantuan untuk mengerjakan soal matematika kelas 9 halaman 264? Tenang, kamu nggak sendirian! Banyak siswa yang juga mengalami kesulitan dalam memahami materi ini. Untuk membantu kamu, kamu bisa mencari referensi di internet, seperti contohnya di kunci jawaban matematika kelas 9 halaman 214 yang bisa kamu akses secara online.
Meskipun halamannya berbeda, tapi konsep dan cara penyelesaiannya bisa menjadi panduan untuk memahami materi halaman 264. Semoga berhasil!
Soal di atas merupakan contoh soal sistem persamaan linear dua variabel. Soal ini mengharuskan siswa untuk mencari nilai x dan y yang memenuhi kedua persamaan.
Rumus dan Konsep yang Relevan
Rumus dan konsep yang relevan dengan soal-soal pada halaman 264 tergantung pada materi yang dibahas. Misalnya, untuk soal sistem persamaan linear dua variabel, rumus yang relevan adalah:
Metode Substitusi
Metode Eliminasi
Metode Grafik
Selain rumus, konsep yang perlu dipahami adalah:
- Pengertian sistem persamaan linear dua variabel
- Cara menyelesaikan sistem persamaan linear dua variabel
- Aplikasi sistem persamaan linear dua variabel dalam kehidupan sehari-hari
Ringkasan Materi, Contoh Soal, dan Rumus
| Materi | Contoh Soal | Rumus |
|---|---|---|
| Sistem Persamaan Linear Dua Variabel | Tentukan himpunan penyelesaian dari sistem persamaan linear dua variabel berikut: 2x + 3y = 7, x
|
Metode Substitusi, Metode Eliminasi, Metode Grafik |
| Fungsi Linear | Tentukan persamaan garis lurus yang melalui titik (2, 3) dan (4, 5) | y = mx + c, m = (y2
|
| Persamaan Kuadrat | Tentukan akar-akar persamaan kuadrat x²
|
Rumus ABC: x = (-b ± √(b²
|
Langkah-Langkah Menyelesaikan Soal
Soal-soal matematika kelas 9 halaman 264 umumnya menguji pemahaman siswa tentang konsep-konsep dasar matematika seperti persamaan linear, sistem persamaan linear, fungsi linear, dan persamaan kuadrat. Untuk menyelesaikan soal-soal tersebut, kamu perlu memahami konsep-konsep dasar dan mengaplikasikannya dalam menyelesaikan soal-soal latihan.
Lagi nyari kunci jawaban matematika kelas 9 halaman 264? Tenang, pasti ada banyak sumber yang bisa kamu akses. Tapi, kalau kamu lagi butuh kunci jawaban untuk pelajaran lain, seperti misalnya kunci jawaban tema 7 kelas 3 halaman 42, kamu bisa cek di situs ini.
Nah, balik lagi ke kunci jawaban matematika kelas 9 halaman 264, pastikan kamu juga memahami konsepnya ya, bukan hanya menghafal jawabannya saja. Selamat belajar!
Langkah-langkah penyelesaian soal pada halaman 264 dapat diuraikan sebagai berikut:
Mengenali Jenis Soal, Kunci jawaban matematika kelas 9 halaman 264
Langkah pertama dalam menyelesaikan soal matematika adalah dengan mengenali jenis soal yang diberikan. Hal ini penting karena akan menentukan langkah-langkah penyelesaian yang tepat. Misalnya, jika soal tersebut merupakan soal persamaan linear, maka langkah penyelesaiannya akan berbeda dengan soal sistem persamaan linear.
Membuat Persamaan
Setelah mengenali jenis soal, langkah selanjutnya adalah membuat persamaan yang sesuai dengan soal. Dalam membuat persamaan, pastikan kamu memahami variabel-variabel yang digunakan dan hubungan antar variabel tersebut. Contohnya, jika soal meminta untuk mencari nilai x dan y, maka kamu perlu membuat dua persamaan yang melibatkan x dan y.
Memecahkan Persamaan
Setelah membuat persamaan, langkah selanjutnya adalah memecahkan persamaan tersebut untuk mencari nilai variabel yang diminta. Dalam memecahkan persamaan, kamu dapat menggunakan berbagai metode, seperti metode eliminasi, substitusi, atau metode grafik. Metode yang digunakan tergantung pada jenis soal dan persamaan yang dibuat.
Menentukan Penyelesaian
Langkah terakhir adalah menentukan penyelesaian dari soal. Penyelesaian dapat berupa nilai variabel yang diminta atau dapat berupa pernyataan yang menjelaskan hasil dari persamaan yang dipecahkan. Pastikan kamu memeriksa kembali jawabanmu untuk memastikan bahwa jawaban yang kamu dapatkan benar dan sesuai dengan soal.
Contoh Soal dan Penyelesaian
Berikut adalah contoh soal dan penyelesaiannya:
Soal 1
Tentukan nilai x dan y yang memenuhi sistem persamaan linear berikut:
2x + 3y = 11
x- 2y = -5
Penyelesaian
Untuk menyelesaikan sistem persamaan linear ini, kita dapat menggunakan metode eliminasi. Langkah-langkahnya adalah sebagai berikut:
- Kalikan persamaan kedua dengan 2, sehingga diperoleh:
- Kurangi persamaan pertama dengan persamaan kedua, sehingga diperoleh:
7y = 21
Sedang mencari kunci jawaban matematika kelas 9 halaman 264? Tenang, kamu nggak sendirian! Banyak yang juga mencari jawaban untuk latihan soal di buku pelajaran. Nah, kalau kamu butuh kunci jawaban untuk pelajaran Bahasa Inggris, bisa cek di kunci jawaban bahasa inggris kelas 9 halaman 14.
Semoga membantu ya! Kembali ke soal matematika, pastikan kamu memahami konsepnya dengan baik, jangan hanya mengandalkan kunci jawaban. Pahami konsep, kerjakan latihan, dan pastinya kamu bisa menyelesaikan soal matematika kelas 9 halaman 264 dengan mudah!
- Bagi kedua ruas dengan 7, sehingga diperoleh:
y = 3
- Substitusikan nilai y = 3 ke persamaan pertama, sehingga diperoleh:
2x + 3(3) = 11
- Sederhanakan persamaan, sehingga diperoleh:
2x + 9 = 11
- Kurangi kedua ruas dengan 9, sehingga diperoleh:
2x = 2
- Bagi kedua ruas dengan 2, sehingga diperoleh:
x = 1
Jadi, nilai x dan y yang memenuhi sistem persamaan linear tersebut adalah x = 1 dan y = 3.
Tabel Langkah-Langkah Penyelesaian
Jenis Soal Langkah 1 Langkah 2 Langkah 3 Langkah 4 Persamaan Linear Mengenali jenis soal Membuat persamaan linear Memecahkan persamaan linear Menentukan penyelesaian Sistem Persamaan Linear Mengenali jenis soal Membuat sistem persamaan linear Memecahkan sistem persamaan linear Menentukan penyelesaian Fungsi Linear Mengenali jenis soal Membuat fungsi linear Menentukan nilai fungsi Menentukan grafik fungsi Persamaan Kuadrat Mengenali jenis soal Membuat persamaan kuadrat Memecahkan persamaan kuadrat Menentukan penyelesaian Pentingnya Memahami Konsep: Kunci Jawaban Matematika Kelas 9 Halaman 264

Memahami konsep dasar matematika sangat penting sebelum kamu mencoba menyelesaikan soal-soal di halaman 264. Hal ini karena konsep dasar matematika menjadi pondasi untuk memahami materi yang lebih kompleks. Jika kamu tidak memahami konsep dasarnya, maka kamu akan kesulitan dalam menyelesaikan soal-soal yang lebih sulit, bahkan yang ada di halaman 264.
Contoh Penerapan Konsep
Misalnya, untuk menyelesaikan soal tentang persamaan linear, kamu harus memahami konsep variabel, koefisien, dan konstanta. Jika kamu tidak memahami konsep-konsep tersebut, kamu akan kesulitan dalam menentukan nilai variabel yang memenuhi persamaan tersebut.
Penerapan Konsep dalam Kehidupan Sehari-hari
Konsep matematika banyak diterapkan dalam kehidupan sehari-hari. Misalnya, ketika kamu membeli barang di toko, kamu menggunakan konsep penjumlahan dan pengurangan untuk menghitung total harga yang harus dibayar. Saat kamu ingin membagi kue dengan teman, kamu menggunakan konsep pembagian.
Ilustrasi Penerapan Konsep Matematika
Bayangkan kamu sedang membangun rumah. Untuk menentukan ukuran dan bentuk rumah, kamu membutuhkan konsep geometri. Untuk menghitung biaya pembangunan, kamu membutuhkan konsep aljabar. Jadi, tanpa memahami konsep matematika, kamu akan kesulitan dalam membangun rumah.
Latihan Soal dan Pembahasan

Untuk menguji pemahaman Anda mengenai materi yang telah dipelajari, mari kita coba beberapa soal latihan. Soal-soal ini mirip dengan soal-soal yang ada di halaman 264 buku teks Anda. Dengan mengerjakan latihan ini, Anda akan semakin terbiasa dalam menyelesaikan soal-soal terkait materi yang telah dipelajari.
Soal Latihan dan Pembahasan
Berikut adalah beberapa soal latihan beserta pembahasannya. Soal-soal ini akan membantu Anda memahami konsep dan mengasah kemampuan dalam menyelesaikan soal-soal yang terkait dengan materi yang telah dipelajari.
No Soal Jawaban Pembahasan 1 Tentukan persamaan garis yang melalui titik (2, 3) dan tegak lurus dengan garis 2x + 3y = 6! y = (3/2)x 2
Garis yang tegak lurus dengan garis 2x + 3y = 6 memiliki gradien yang merupakan negatif dari kebalikan gradien garis tersebut. Gradien garis 2x + 3y = 6 adalah - 2/
- Oleh karena itu, gradien garis yang tegak lurus adalah (3/2). Persamaan garis yang melalui titik (2, 3) dengan gradien (3/2) adalah: y
- 3 = (3/2)(x
- 2) y = (3/2)x
- 2.
2 Tentukan persamaan garis yang sejajar dengan garis y = 2x + 5 dan melalui titik (1, 4)! y = 2x + 2 Garis yang sejajar dengan garis y = 2x + 5 memiliki gradien yang sama dengan gradien garis tersebut. Gradien garis y = 2x + 5 adalah - Oleh karena itu, gradien garis yang sejajar adalah
- Persamaan garis yang melalui titik (1, 4) dengan gradien 2 adalah: y
- 4 = 2(x
- 1) y = 2x + 2.
3 Tentukan jarak titik (3, 4) ke garis 3x + 4y 12 = 0!
1 Jarak titik (x1, y1) ke garis ax + by + c = 0 dapat dihitung dengan rumus: d = |ax1 + by1 + c| / √(a^2 + b^2). Dalam kasus ini, x1 = 3, y1 = 4, a = 3, b = 4, dan c = - Dengan substitusi ke dalam rumus, kita dapatkan: d = |(3)(3) + (4)(4)
- 12| / √(3^2 + 4^2) = 1.
Ringkasan Akhir

Dengan memahami konsep dan langkah-langkah yang benar, kamu akan mampu menyelesaikan soal-soal matematika di halaman 264 dengan percaya diri. Ingat, kunci utama dalam belajar matematika adalah latihan dan konsistensi. Jangan ragu untuk mengulang materi dan mencoba latihan soal lainnya untuk menguji pemahamanmu.
Selamat belajar!
Informasi FAQ
Apakah kunci jawaban ini benar?
Kunci jawaban ini dibuat berdasarkan pemahaman konsep dan langkah-langkah yang benar dalam menyelesaikan soal. Namun, disarankan untuk selalu berkonsultasi dengan guru atau sumber belajar lain untuk memastikan keakuratannya.
Apakah kunci jawaban ini sesuai dengan buku pelajaran?
Kunci jawaban ini dibuat berdasarkan soal-soal yang terdapat di halaman 264 buku pelajaran matematika kelas 9. Pastikan kamu menggunakan buku pelajaran yang sama.
2x- 4y = -10