Kunci jawaban matematika kelas 9 halaman 255 – Pernahkah kamu merasa kesulitan dalam menyelesaikan soal-soal matematika di halaman 255 buku teks kelas 9? Tenang, kamu tidak sendirian! Banyak siswa yang merasa tertantang dengan materi di halaman tersebut. Artikel ini hadir untuk membantu kamu memahami konsep-konsep matematika yang diujikan dan memberikan solusi lengkap untuk setiap soal.
Dengan panduan langkah demi langkah yang mudah dipahami, kamu akan dapat menaklukkan semua tantangan di halaman 255.
Kita akan membahas berbagai topik matematika yang diujikan, mulai dari persamaan linear hingga geometri. Setiap soal akan dilengkapi dengan pembahasan yang detail, sehingga kamu dapat memahami proses penyelesaiannya dengan mudah. Selain itu, artikel ini juga akan memberikan tips dan trik jitu untuk menyelesaikan soal-soal matematika dengan lebih cepat dan akurat.
Soal-Soal Matematika Kelas 9 Halaman 255
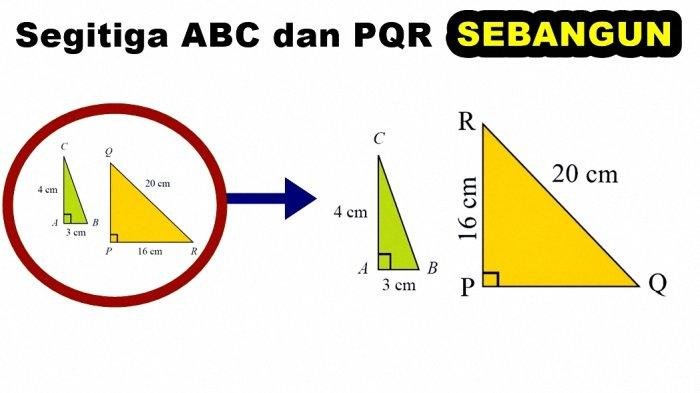
Halaman 255 buku teks matematika kelas 9 berisi soal-soal yang menguji pemahaman siswa tentang berbagai konsep matematika. Soal-soal ini dirancang untuk membantu siswa mengasah kemampuan mereka dalam menyelesaikan masalah matematika, baik yang bersifat teoritis maupun aplikatif.
Berikut adalah tabel yang berisi rincian soal-soal matematika di halaman 255, termasuk jenis soal dan topik yang diujikan:
Daftar Soal Matematika Halaman 255
| Nomor Soal | Jenis Soal | Topik |
|---|---|---|
| 1 | Pilihan Ganda | Persamaan Linear Dua Variabel |
| 2 | Pilihan Ganda | Sistem Persamaan Linear Dua Variabel |
| 3 | Pilihan Ganda | Pertidaksamaan Linear Dua Variabel |
| 4 | Pilihan Ganda | Sistem Pertidaksamaan Linear Dua Variabel |
| 5 | Esai | Menyelesaikan Sistem Persamaan Linear Dua Variabel dengan Metode Substitusi |
| 6 | Esai | Menyelesaikan Sistem Persamaan Linear Dua Variabel dengan Metode Eliminasi |
| 7 | Esai | Menyelesaikan Sistem Pertidaksamaan Linear Dua Variabel dengan Metode Grafik |
| 8 | Esai | Penerapan Sistem Persamaan Linear Dua Variabel dalam Masalah Kontekstual |
Persamaan Linear Dua Variabel
Soal nomor 1 menguji pemahaman siswa tentang konsep persamaan linear dua variabel. Persamaan linear dua variabel adalah persamaan yang memuat dua variabel dengan pangkat tertinggi satu. Contohnya, persamaan 2x + 3y = 6 adalah persamaan linear dua variabel. Soal ini mungkin meminta siswa untuk menentukan apakah suatu persamaan merupakan persamaan linear dua variabel atau tidak, atau untuk menentukan nilai variabel tertentu dalam persamaan linear dua variabel.
Sistem Persamaan Linear Dua Variabel
Soal nomor 2 menguji pemahaman siswa tentang konsep sistem persamaan linear dua variabel. Sistem persamaan linear dua variabel adalah kumpulan dua atau lebih persamaan linear yang memuat variabel yang sama. Contohnya, sistem persamaan 2x + 3y = 6 dan x – y = 1 adalah sistem persamaan linear dua variabel.
Soal ini mungkin meminta siswa untuk menentukan solusi dari sistem persamaan linear dua variabel, atau untuk menentukan apakah suatu pasangan nilai merupakan solusi dari sistem persamaan linear dua variabel.
Pertidaksamaan Linear Dua Variabel
Soal nomor 3 menguji pemahaman siswa tentang konsep pertidaksamaan linear dua variabel. Pertidaksamaan linear dua variabel adalah pertidaksamaan yang memuat dua variabel dengan pangkat tertinggi satu. Contohnya, pertidaksamaan 2x + 3y < 6 adalah pertidaksamaan linear dua variabel. Soal ini mungkin meminta siswa untuk menentukan apakah suatu pertidaksamaan merupakan pertidaksamaan linear dua variabel atau tidak, atau untuk menentukan himpunan penyelesaian dari pertidaksamaan linear dua variabel.
Sistem Pertidaksamaan Linear Dua Variabel, Kunci jawaban matematika kelas 9 halaman 255
Soal nomor 4 menguji pemahaman siswa tentang konsep sistem pertidaksamaan linear dua variabel. Sistem pertidaksamaan linear dua variabel adalah kumpulan dua atau lebih pertidaksamaan linear yang memuat variabel yang sama. Contohnya, sistem pertidaksamaan 2x + 3y < 6 dan x - y > 1 adalah sistem pertidaksamaan linear dua variabel. Soal ini mungkin meminta siswa untuk menentukan himpunan penyelesaian dari sistem pertidaksamaan linear dua variabel, atau untuk menentukan apakah suatu pasangan nilai merupakan solusi dari sistem pertidaksamaan linear dua variabel.
Menyelesaikan Sistem Persamaan Linear Dua Variabel
Soal nomor 5 dan 6 menguji kemampuan siswa dalam menyelesaikan sistem persamaan linear dua variabel. Soal ini dapat diselesaikan dengan menggunakan beberapa metode, seperti metode substitusi, metode eliminasi, atau metode grafik. Metode substitusi melibatkan mengganti salah satu variabel dalam satu persamaan dengan ekspresi yang setara dari persamaan lainnya.
Metode eliminasi melibatkan mengeliminasi salah satu variabel dengan mengalikan kedua persamaan dengan konstanta yang sesuai dan kemudian menjumlahkan atau mengurangkan kedua persamaan. Metode grafik melibatkan menggambarkan kedua persamaan pada bidang cartesius dan menentukan titik potong kedua grafik.
Menyelesaikan Sistem Pertidaksamaan Linear Dua Variabel
Soal nomor 7 menguji kemampuan siswa dalam menyelesaikan sistem pertidaksamaan linear dua variabel. Soal ini dapat diselesaikan dengan menggunakan metode grafik. Metode grafik melibatkan menggambarkan kedua pertidaksamaan pada bidang cartesius dan menentukan daerah yang memenuhi semua pertidaksamaan. Daerah yang memenuhi semua pertidaksamaan merupakan himpunan penyelesaian dari sistem pertidaksamaan linear dua variabel.
Penerapan Sistem Persamaan Linear Dua Variabel dalam Masalah Kontekstual
Soal nomor 8 menguji kemampuan siswa dalam menerapkan konsep sistem persamaan linear dua variabel dalam masalah kontekstual. Soal ini biasanya berbentuk cerita yang melibatkan dua atau lebih variabel yang saling terkait. Siswa diminta untuk membuat model matematika dari masalah kontekstual dan menyelesaikannya dengan menggunakan sistem persamaan linear dua variabel.
Solusi dan Pembahasan Soal

Selamat datang kembali! Pada artikel ini, kita akan membahas solusi dan pembahasan soal matematika yang terdapat di halaman 255. Mari kita bahas satu per satu dengan langkah-langkah yang jelas dan mudah dipahami.
Soal 1: Menentukan Persamaan Garis Lurus
Soal ini meminta kita untuk menentukan persamaan garis lurus yang melalui titik (2, 3) dan tegak lurus dengan garis 2x + 3y = 6. Untuk menyelesaikan soal ini, kita perlu memahami konsep gradien dan persamaan garis lurus.
- Langkah pertama adalah mencari gradien garis 2x + 3y = 6. Kita bisa melakukannya dengan mengubah persamaan tersebut ke bentuk y = mx + c, di mana m adalah gradien. Setelah diubah, persamaannya menjadi y = (-2/3)x + 2.
Jadi, gradien garis tersebut adalah -2/3.
- Karena garis yang kita cari tegak lurus dengan garis 2x + 3y = 6, maka gradiennya adalah negatif kebalikan dari gradien garis tersebut. Artinya, gradien garis yang kita cari adalah 3/2.
- Selanjutnya, kita gunakan rumus persamaan garis lurus y – y1 = m(x – x1), dengan (x1, y1) adalah titik yang dilalui garis dan m adalah gradien. Substitusikan nilai (2, 3) dan 3/2 ke dalam rumus tersebut, kita dapatkan y – 3 = (3/2)(x – 2).
Setelah disederhanakan, persamaan garis lurus yang kita cari adalah 3x – 2y = 0.
Soal 2: Menentukan Nilai x dan y
Soal ini meminta kita untuk menentukan nilai x dan y yang memenuhi sistem persamaan berikut:
x + 2y = 5
- x
- y = 1
Untuk menyelesaikan soal ini, kita dapat menggunakan metode eliminasi atau substitusi. Berikut adalah langkah-langkah menggunakan metode eliminasi:
- Kalikan persamaan pertama dengan 2, sehingga menjadi 2x + 4y = 10.
- Kurangi persamaan kedua dari persamaan pertama, sehingga kita dapatkan 5y = 9.
- Dari persamaan 5y = 9, kita dapatkan y = 9/5.
- Substitusikan nilai y = 9/5 ke dalam salah satu persamaan awal, misalnya x + 2y = 5. Kita dapatkan x + 2(9/5) = 5. Setelah disederhanakan, kita dapatkan x = 1/5.
Jadi, nilai x dan y yang memenuhi sistem persamaan tersebut adalah x = 1/5 dan y = 9/5.
Soal 3: Menentukan Luas Segitiga
Soal ini meminta kita untuk menentukan luas segitiga ABC dengan titik-titik A(1, 2), B(4, 5), dan C(7, 2). Untuk menyelesaikan soal ini, kita dapat menggunakan rumus luas segitiga dengan koordinat titik-titiknya.
Luas Segitiga = 1/2 |(x1(y2
- y3) + x2(y3
- y1) + x3(y1
- y2))|
Substitusikan koordinat titik A, B, dan C ke dalam rumus tersebut, kita dapatkan:
Luas Segitiga ABC = 1/2 |(1(5
- 2) + 4(2
- 2) + 7(2
- 5))| = 1/2 |(3 + 0
- 21)| = 9
Jadi, luas segitiga ABC adalah 9 satuan luas.
Konsep Matematika yang Relevan
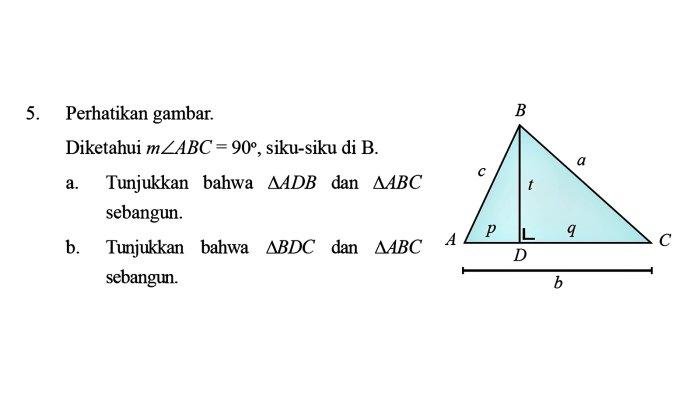
Soal-soal di halaman 255 buku matematika kelas 9 menguji pemahaman siswa tentang beberapa konsep matematika penting. Konsep-konsep ini saling terkait dan membentuk dasar pemahaman matematika yang lebih kompleks. Berikut adalah beberapa konsep matematika yang relevan dengan soal-soal di halaman 255:
Persamaan Linear Dua Variabel
Persamaan linear dua variabel merupakan persamaan yang memiliki dua variabel dengan pangkat tertinggi satu. Persamaan ini dapat ditulis dalam bentuk umum:
ax + by = c
di mana a, b, dan c adalah konstanta, dan x dan y adalah variabel.Persamaan linear dua variabel dapat direpresentasikan dalam bentuk grafik. Grafik persamaan linear dua variabel adalah garis lurus. Contoh:Persamaan 2x + 3y = 6 adalah persamaan linear dua variabel.
Lagi-lagi butuh bantuan untuk mengerjakan soal matematika kelas 9 halaman 255? Tenang, kamu nggak sendirian! Banyak yang merasa kesulitan, terutama kalau soal-soalnya rumit. Tapi, sebelum kamu menyerah, coba deh cari tahu tips dan trik mengerjakan soal-soal tersebut. Kalau kamu sedang mencari kunci jawaban untuk TOEFL Section 2 Structure and Written Expression, kamu bisa coba kunjungi kunci jawaban toefl section 2 structure and written expression untuk referensi.
Nah, setelah itu, kamu bisa fokus lagi ke soal matematika kelas 9 halaman 255 dan coba selesaikan dengan lebih percaya diri!
Grafik persamaan ini adalah garis lurus yang memotong sumbu x di titik (3, 0) dan sumbu y di titik (0, 2).
Sistem Persamaan Linear Dua Variabel
Sistem persamaan linear dua variabel adalah kumpulan dua atau lebih persamaan linear dengan variabel yang sama. Contoh:Sistem persamaan linear dua variabel berikut:
x + 3y = 6
x
y = 1
Sistem persamaan ini memiliki solusi (x, y) yang memenuhi kedua persamaan tersebut.
Metode Penyelesaian Sistem Persamaan Linear Dua Variabel
Ada beberapa metode yang dapat digunakan untuk menyelesaikan sistem persamaan linear dua variabel, yaitu:
- Metode Substitusi
- Metode Eliminasi
- Metode Grafik
Contoh:Sistem persamaan linear dua variabel berikut:
x + 3y = 6
x
y = 1
dapat diselesaikan dengan menggunakan metode substitusi.
Bingung sama soal matematika kelas 9 halaman 255? Tenang, banyak kok sumber belajar yang bisa kamu akses! Mungkin kamu juga bisa mencari referensi dari kunci jawaban tema 6 kelas 6 halaman 102 yang membahas materi serupa. Dengan memahami konsepnya, pasti kamu bisa ngerjain soal matematika kelas 9 halaman 255 dengan mudah!
1. Metode Substitusi
Selesaikan salah satu persamaan untuk salah satu variabel. Misalnya, selesaikan persamaan kedua untuk x:
x = y + 1
Substitusikan nilai x ini ke persamaan pertama:
2(y + 1) + 3y = 6
Selesaikan persamaan untuk y:
2y + 2 + 3y = 6 5y = 4 y = 4/5
Substitusikan nilai y ini ke persamaan kedua untuk mendapatkan nilai x:
x
4/5 = 1
x = 9/5
Jadi, solusi sistem persamaan ini adalah (x, y) = (9/5, 4/5).
Bingung dengan soal matematika kelas 9 halaman 255? Tenang, banyak kok yang mengalami hal yang sama. Mungkin kamu juga sedang mencari kunci jawaban bahasa indonesia kelas 12 halaman 139 ya? Nah, untuk soal matematika kelas 9 halaman 255, coba cek lagi rumus dan konsepnya, pasti bisa dipecahkan!
2. Metode Eliminasi
Kalikan kedua persamaan dengan konstanta sehingga koefisien salah satu variabel menjadi sama. Misalnya, kalikan persamaan kedua dengan 3:
3x
3y = 3
Jumlahkan kedua persamaan:
2x + 3y = 6 3x
3y = 3
————
5x = 9
Selesaikan persamaan untuk x:
x = 9/5
Substitusikan nilai x ini ke salah satu persamaan awal untuk mendapatkan nilai y:
9/5
y = 1
y = 4/5
Jadi, solusi sistem persamaan ini adalah (x, y) = (9/5, 4/5).
3. Metode Grafik
Gambar grafik kedua persamaan linear pada sistem persamaan. Titik potong kedua grafik adalah solusi sistem persamaan.
Pertidaksamaan Linear Dua Variabel
Pertidaksamaan linear dua variabel merupakan pertidaksamaan yang memiliki dua variabel dengan pangkat tertinggi satu. Pertidaksamaan ini dapat ditulis dalam bentuk umum:
ax + by > cax + by < c ax + by ≥ c ax + by ≤ c
di mana a, b, dan c adalah konstanta, dan x dan y adalah variabel.Pertidaksamaan linear dua variabel dapat direpresentasikan dalam bentuk grafik. Grafik pertidaksamaan linear dua variabel adalah daerah yang memenuhi pertidaksamaan tersebut. Contoh:Pertidaksamaan 2x + 3y > 6 adalah pertidaksamaan linear dua variabel.
Grafik pertidaksamaan ini adalah daerah di atas garis 2x + 3y = 6.
Sistem Pertidaksamaan Linear Dua Variabel, Kunci jawaban matematika kelas 9 halaman 255
Sistem pertidaksamaan linear dua variabel adalah kumpulan dua atau lebih pertidaksamaan linear dengan variabel yang sama. Contoh:Sistem pertidaksamaan linear dua variabel berikut:
x + 3y > 6
x- y < 1
Sistem pertidaksamaan ini memiliki solusi (x, y) yang memenuhi semua pertidaksamaan tersebut.
Metode Penyelesaian Sistem Pertidaksamaan Linear Dua Variabel
Untuk menyelesaikan sistem pertidaksamaan linear dua variabel, langkah-langkahnya adalah:
- Gambar grafik setiap pertidaksamaan pada sistem pertidaksamaan.
- Tentukan daerah yang memenuhi semua pertidaksamaan.
Contoh:Sistem pertidaksamaan linear dua variabel berikut:
x + 3y > 6
x- y < 1
dapat diselesaikan dengan menggunakan metode grafik.
1. Gambar grafik setiap pertidaksamaan
Gambar grafik pertidaksamaan 2x + 3y > 6. Daerah yang memenuhi pertidaksamaan ini adalah daerah di atas garis 2x + 3y = 6. Gambar grafik pertidaksamaan x- y < 1. Daerah yang memenuhi pertidaksamaan ini adalah daerah di bawah garis x - y = 1. 2. Tentukan daerah yang memenuhi semua pertidaksamaan:Daerah yang memenuhi semua pertidaksamaan adalah daerah yang di arsir pada kedua grafik.
Contoh Penerapan Konsep Matematika dalam Kehidupan Sehari-hari
Konsep matematika yang dibahas di atas memiliki banyak aplikasi dalam kehidupan sehari-hari. Misalnya:
- Persamaan linear dua variabel dapat digunakan untuk menghitung biaya total pembelian suatu barang dengan harga tertentu.
- Sistem persamaan linear dua variabel dapat digunakan untuk menyelesaikan masalah pencampuran, seperti menentukan jumlah air dan gula yang diperlukan untuk membuat larutan dengan konsentrasi tertentu.
- Pertidaksamaan linear dua variabel dapat digunakan untuk menentukan batas maksimum dan minimum suatu variabel, seperti menentukan jumlah maksimum barang yang dapat diproduksi dengan sumber daya yang terbatas.
- Sistem pertidaksamaan linear dua variabel dapat digunakan untuk menentukan area yang memenuhi beberapa persyaratan, seperti menentukan area yang aman untuk pembangunan suatu bangunan.
Tips dan Trik Menyelesaikan Soal

Soal-soal matematika di halaman 255 buku teks kelas 9 mungkin tampak menantang, tetapi dengan strategi yang tepat, kamu dapat mengatasinya dengan mudah. Berikut beberapa tips dan trik yang dapat membantu kamu menyelesaikan soal-soal tersebut.
Memahami Konsep Dasar
Sebelum kamu mulai mengerjakan soal, pastikan kamu memahami konsep dasar yang terkait dengan soal tersebut. Misalnya, jika soal tentang persamaan linear, pastikan kamu memahami cara menyelesaikan persamaan linear. Kamu dapat meninjau kembali catatan kelas atau buku teks untuk membantu memahami konsep-konsep ini.
Menganalisis Soal
Setelah kamu memahami konsep dasar, langkah selanjutnya adalah menganalisis soal. Baca soal dengan cermat dan identifikasi informasi penting yang diberikan. Tuliskan informasi tersebut dan tentukan apa yang ingin kamu cari.
Memilih Strategi yang Tepat
Ada banyak strategi yang dapat kamu gunakan untuk menyelesaikan soal matematika. Pilih strategi yang paling tepat untuk soal yang kamu kerjakan. Misalnya, jika soal tentang persamaan linear, kamu dapat menggunakan metode eliminasi, substitusi, atau grafik.
Mencoba Soal Latihan
Setelah kamu memahami konsep dasar dan memilih strategi yang tepat, cobalah mengerjakan soal latihan. Soal latihan dapat membantu kamu mempraktikkan strategi yang kamu pilih dan mengidentifikasi area yang perlu kamu perbaiki.
Memeriksa Jawaban
Setelah kamu menyelesaikan soal, jangan lupa untuk memeriksa jawaban kamu. Pastikan jawaban kamu masuk akal dan sesuai dengan informasi yang diberikan dalam soal. Kamu juga dapat menggunakan kalkulator untuk membantu memeriksa jawaban kamu.
Tips dan Trik yang Paling Efektif
Ketika menghadapi soal yang sulit, cobalah untuk memecah soal menjadi bagian-bagian yang lebih kecil. Ini dapat membantu kamu fokus pada satu bagian dari soal pada satu waktu dan membuat soal lebih mudah dipahami.
Jika kamu kesulitan memahami soal, cobalah untuk membuat diagram atau gambar. Ini dapat membantu kamu memvisualisasikan soal dan membuat solusi lebih jelas.
Jangan takut untuk meminta bantuan. Jika kamu mengalami kesulitan dengan soal, tanyakan kepada guru atau teman sekelas kamu untuk mendapatkan bantuan.
Kesimpulan Akhir: Kunci Jawaban Matematika Kelas 9 Halaman 255
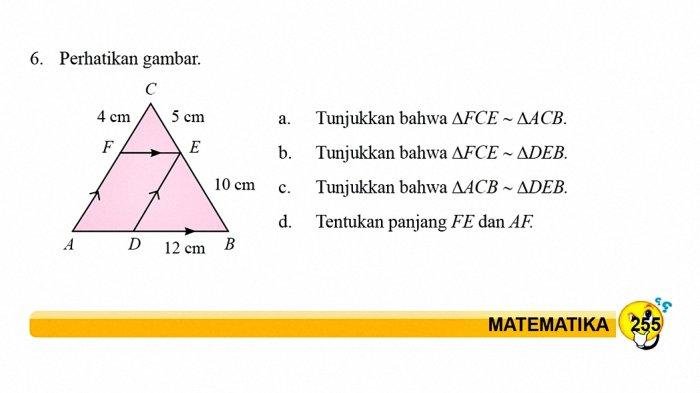
Dengan memahami konsep-konsep matematika yang diujikan di halaman 255, kamu akan memiliki dasar yang kuat untuk menghadapi materi selanjutnya. Jangan ragu untuk meninjau kembali pembahasan ini jika kamu mengalami kesulitan. Ingat, belajar matematika adalah proses yang berkelanjutan. Dengan latihan dan pemahaman yang baik, kamu akan dapat menguasai materi ini dengan mudah.
FAQ Terpadu
Apakah kunci jawaban ini cocok untuk semua buku teks matematika kelas 9?
Kunci jawaban ini dirancang khusus untuk buku teks matematika kelas 9 yang membahas materi di halaman 255. Namun, konsep-konsep yang dibahas dalam artikel ini umumnya berlaku untuk semua buku teks matematika kelas 9.
Apakah ada latihan soal tambahan yang bisa saya kerjakan?
Ya, kamu dapat menemukan latihan soal tambahan di buku teks matematika kelas 9, buku latihan, atau website online. Gunakan latihan soal ini untuk menguji pemahamanmu dan meningkatkan kemampuanmu dalam menyelesaikan soal matematika.