Kunci jawaban matematika kelas 9 halaman 239 nomor 4 – Pernahkah kamu merasa kesulitan memahami soal matematika kelas 9 halaman 239 nomor 4? Soal ini menguji pemahaman tentang konsep matematika yang penting dan sering muncul dalam kehidupan sehari-hari. Artikel ini akan membantumu memahami soal tersebut dengan langkah-langkah penyelesaian yang jelas, serta memberikan contoh penerapan konsep dalam kehidupan nyata.
Mari kita mulai dengan memahami konteks soal dan konsep matematika yang diuji. Kemudian, kita akan membahas langkah-langkah penyelesaian dengan menggunakan rumus yang tepat dan memberikan penjelasan detail untuk setiap langkah. Setelah itu, kita akan melihat bagaimana pemahaman konsep ini dapat membantu dalam menyelesaikan soal-soal serupa dan penerapannya dalam kehidupan sehari-hari.
Memahami Soal
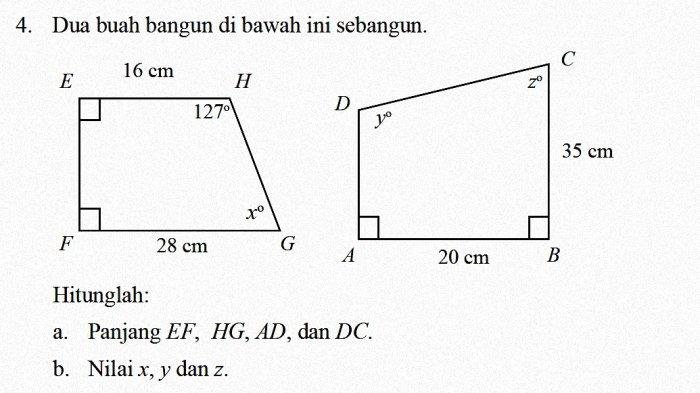
Soal matematika kelas 9 halaman 239 nomor 4 membahas tentang penerapan konsep trigonometri dalam menghitung tinggi suatu bangunan. Soal ini menyajikan skenario di mana seseorang mengamati puncak bangunan dari suatu titik tertentu dengan sudut elevasi tertentu.
Bingung sama soal matematika kelas 9 halaman 239 nomor 4? Tenang, banyak kok yang ngalamin hal serupa! Nah, buat yang lagi nyari kunci jawaban bahasa Indonesia kelas 8 halaman 159, bisa langsung cek di kunci jawaban bahasa indonesia kelas 8 halaman 159.
Semoga bermanfaat ya! Nah, balik lagi ke soal matematika kelas 9 halaman 239 nomor 4, coba deh cek lagi rumus-rumusnya, pasti bisa dikerjain kok!
Langkah-langkah Penyelesaian Soal
Untuk menyelesaikan soal ini, kita perlu mengikuti langkah-langkah berikut:
- Menganalisis soal dan mengidentifikasi informasi yang diberikan. Dalam soal ini, kita diberikan sudut elevasi dan jarak horizontal dari titik pengamatan ke kaki bangunan.
- Menggambar diagram sketsa yang menggambarkan situasi yang dijelaskan dalam soal. Diagram ini akan membantu kita memvisualisasikan hubungan antara sudut, sisi-sisi segitiga, dan tinggi bangunan yang ingin kita cari.
- Memilih rumus trigonometri yang tepat untuk menyelesaikan masalah. Karena kita memiliki sudut dan sisi yang berhadapan dengan sudut tersebut (sisi miring), kita dapat menggunakan rumus sinus.
- Menghitung tinggi bangunan dengan menggunakan rumus sinus dan nilai trigonometri yang telah kita ketahui. Rumus sinus menyatakan bahwa sinus suatu sudut sama dengan perbandingan sisi yang berhadapan dengan sudut tersebut terhadap sisi miring segitiga.
Konsep Matematika yang Diuji
Soal ini menguji pemahaman siswa tentang konsep trigonometri, khususnya tentang:
- Sudut elevasi: Sudut elevasi adalah sudut yang dibentuk antara garis horizontal dan garis pandang ke suatu objek yang berada di atas garis horizontal.
- Rumus sinus: Rumus sinus digunakan untuk menghitung perbandingan antara sisi yang berhadapan dengan sudut dan sisi miring dalam segitiga siku-siku.
- Penerapan trigonometri dalam masalah kontekstual: Soal ini menunjukkan bagaimana trigonometri dapat digunakan untuk menyelesaikan masalah nyata seperti menghitung tinggi bangunan.
Penyelesaian Soal
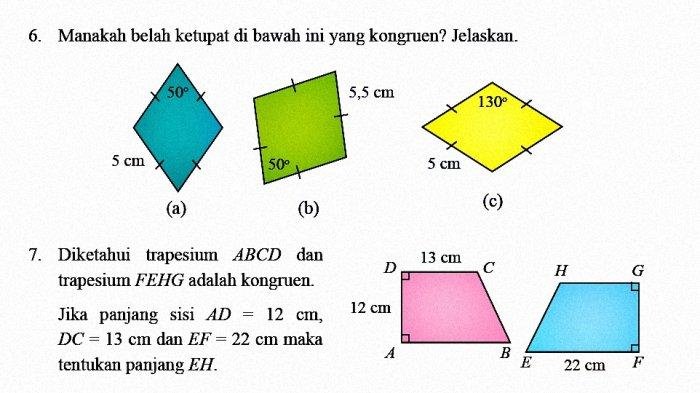
Soal nomor 4 pada halaman 239 buku Matematika kelas 9 membahas tentang penerapan konsep persamaan kuadrat dalam menyelesaikan masalah kontekstual. Soal ini mengajak kita untuk menganalisis dan menentukan hubungan antara variabel yang terlibat dalam masalah, kemudian menyusun persamaan kuadrat yang sesuai untuk mencari solusi.
Sedang mencari kunci jawaban matematika kelas 9 halaman 239 nomor 4? Tenang, banyak sumber belajar yang bisa kamu akses. Ingat, memahami konsep lebih penting daripada sekadar melihat kunci jawaban. Kamu juga bisa cari referensi di website kunci jawaban agama islam kelas 9 halaman 22 untuk bahan belajar agamamu.
Kembali ke soal matematika, pastikan kamu memahami setiap langkah penyelesaiannya agar kamu bisa menerapkannya di soal-soal lain. Semangat belajar!
Langkah-langkah Penyelesaian Soal
Berikut langkah-langkah penyelesaian soal nomor 4:
- Menentukan variabel yang terlibat dalam soal. Dalam soal ini, variabel yang terlibat adalah panjang dan lebar persegi panjang. Misalkan panjang persegi panjang adalah ‘p’ dan lebarnya adalah ‘l’.
- Menyusun persamaan berdasarkan informasi yang diberikan dalam soal. Dari soal diketahui bahwa panjang persegi panjang 5 cm lebih panjang dari lebarnya, sehingga dapat ditulis sebagai p = l + 5. Selain itu, diketahui luas persegi panjang adalah 84 cm2, sehingga dapat ditulis sebagai p
l = 84.
- Mensubstitusikan persamaan pertama (p = l + 5) ke persamaan kedua (pl = 84). Substitusi ini dilakukan untuk menghilangkan variabel ‘p’ dan menghasilkan persamaan kuadrat dalam satu variabel, yaitu ‘l’.
- Memecahkan persamaan kuadrat yang diperoleh dengan menggunakan metode pemfaktoran, rumus kuadrat, atau metode lain yang sesuai. Dalam kasus ini, kita dapat menggunakan metode pemfaktoran.
- Setelah mendapatkan nilai ‘l’ (lebar), substitusikan nilai tersebut ke persamaan p = l + 5 untuk mendapatkan nilai ‘p’ (panjang).
Tabel Data dan Hasil Perhitungan
| Variabel | Nilai | Keterangan |
|---|---|---|
| p (panjang) | 12 cm | Diperoleh setelah mensubstitusikan nilai ‘l’ ke persamaan p = l + 5 |
| l (lebar) | 7 cm | Diperoleh dari penyelesaian persamaan kuadrat |
| Luas | 84 cm2 | Diketahui dalam soal |
Penjelasan Detail
Berikut penjelasan detail untuk setiap langkah penyelesaian soal:
- Menentukan variabel: Variabel yang terlibat dalam soal adalah panjang dan lebar persegi panjang. Panjang dilambangkan dengan ‘p’ dan lebar dilambangkan dengan ‘l’.
- Menyusun persamaan: Dari soal diketahui bahwa panjang 5 cm lebih panjang dari lebar, sehingga p = l + 5. Luas persegi panjang adalah p
l = 84.
- Substitusi: Substitusikan p = l + 5 ke persamaan p
- l = 84. Maka diperoleh (l + 5)
- l = 84.
- Penyelesaian Persamaan Kuadrat: Persamaan (l + 5)
- l = 84 dapat diubah menjadi l 2+ 5l
- 84 = 0. Persamaan ini dapat difaktorkan menjadi (l + 12)(l
- 7) = 0. Maka diperoleh l =
- 12 atau l = 7. Karena lebar tidak mungkin bernilai negatif, maka l = 7 cm.
- Mencari Panjang: Setelah diperoleh l = 7 cm, substitusikan nilai tersebut ke persamaan p = l + 5. Maka diperoleh p = 7 + 5 = 12 cm.
Pentingnya Memahaman Konsep

Dalam matematika, memahami konsep merupakan kunci utama untuk menyelesaikan soal dengan mudah dan efektif. Ketika kita hanya menghafal rumus tanpa memahami konsep di baliknya, kita akan kesulitan dalam menghadapi soal-soal yang sedikit berbeda atau lebih kompleks. Memahami konsep membantu kita dalam memahami hubungan antara berbagai ide matematika dan bagaimana mereka saling terkait.
Hal ini memungkinkan kita untuk menyelesaikan soal dengan lebih fleksibel dan kreatif, bahkan ketika menghadapi soal yang belum pernah kita temui sebelumnya.
Contoh Soal dan Penerapan Konsep
Sebagai contoh, mari kita tinjau soal kelas 9 halaman 239 nomor 4. Soal ini membahas tentang persamaan garis lurus. Memahami konsep persamaan garis lurus, seperti gradien dan titik potong, membantu kita dalam menyelesaikan soal ini dengan lebih mudah. Kita dapat menggunakan konsep gradien untuk menentukan kemiringan garis, dan titik potong untuk menentukan titik di mana garis memotong sumbu koordinat.
Dengan memahami konsep ini, kita dapat dengan mudah menentukan persamaan garis lurus yang memenuhi syarat yang diberikan dalam soal.
- Misalnya, jika kita diberikan dua titik pada garis lurus, kita dapat menggunakan konsep gradien untuk menentukan kemiringan garis tersebut. Kemudian, kita dapat menggunakan salah satu titik dan gradien yang telah kita temukan untuk menentukan persamaan garis lurus tersebut.
- Jika kita diberikan persamaan garis lurus, kita dapat menggunakan konsep gradien dan titik potong untuk menentukan kemiringan dan titik potong garis tersebut. Informasi ini dapat membantu kita dalam menggambar garis lurus tersebut pada bidang koordinat.
Penerapan dalam Kehidupan Sehari-hari
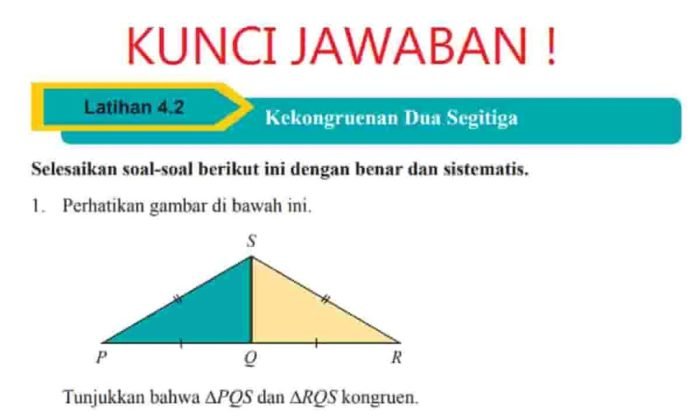
Konsep matematika yang diuji dalam soal ini memiliki aplikasi luas dalam kehidupan sehari-hari, khususnya dalam bidang keuangan dan perencanaan. Konsep tersebut membantu kita memahami dan mengelola keuangan dengan lebih efektif, serta membuat keputusan yang tepat terkait investasi dan pengeluaran.
Perencanaan Keuangan Pribadi
Konsep matematika yang dibahas dalam soal dapat diaplikasikan dalam perencanaan keuangan pribadi, misalnya dalam menghitung bunga tabungan atau pinjaman.
- Misalnya, jika seseorang menabung sejumlah uang di bank dengan bunga tertentu, konsep persentase dan perhitungan bunga majemuk dapat digunakan untuk menghitung total tabungan setelah jangka waktu tertentu.
- Konsep ini juga membantu dalam menghitung cicilan pinjaman, biaya asuransi, dan investasi.
Pengambilan Keputusan Investasi
Konsep matematika yang dibahas dalam soal dapat membantu dalam membuat keputusan investasi yang bijak.
- Misalnya, jika seseorang ingin berinvestasi di saham atau obligasi, konsep persentase dan perhitungan pengembalian investasi (ROI) dapat digunakan untuk membandingkan berbagai pilihan investasi dan memilih yang paling menguntungkan.
- Konsep ini juga membantu dalam menghitung risiko investasi dan menentukan strategi investasi yang tepat.
Perencanaan Anggaran
Konsep matematika yang dibahas dalam soal dapat membantu dalam merencanakan anggaran dengan lebih efektif.
Lagi-lagi nyangkut di soal matematika kelas 9 halaman 239 nomor 4? Tenang, pasti ada jalan keluarnya! Meskipun soal matematika ini mungkin sedikit menantang, kamu bisa coba cari referensi di internet. Atau, kalau lagi butuh tambahan referensi, coba cek juga kunci jawaban ipa kelas 9 halaman 8 kurikulum merdeka.
Siapa tahu ada konsep atau rumus yang bisa kamu gunakan untuk menyelesaikan soal matematika kelas 9 halaman 239 nomor 4 ini. Semangat, ya!
- Misalnya, dengan memahami konsep persentase dan perhitungan proporsi, seseorang dapat mengalokasikan pengeluaran untuk kebutuhan pokok, seperti makanan, tempat tinggal, dan transportasi, dengan lebih tepat.
- Konsep ini juga membantu dalam menghitung pengeluaran bulanan dan menentukan target penghematan.
Perencanaan Bisnis
Konsep matematika yang dibahas dalam soal juga memiliki aplikasi dalam perencanaan bisnis, seperti dalam menghitung biaya produksi, menentukan harga jual, dan menganalisis profitabilitas.
- Misalnya, dalam menghitung biaya produksi, konsep persentase dan perhitungan proporsi dapat digunakan untuk menentukan biaya bahan baku, tenaga kerja, dan overhead.
- Konsep ini juga membantu dalam menghitung margin keuntungan dan menentukan strategi penetapan harga yang tepat.
Ilustrasi Penerapan Konsep, Kunci jawaban matematika kelas 9 halaman 239 nomor 4
Sebagai ilustrasi, perhatikan contoh berikut. Seorang karyawan ingin menabung untuk membeli rumah dengan harga Rp500 juta. Dia ingin menabung selama 5 tahun dengan bunga tabungan 5% per tahun. Dengan menggunakan konsep persentase dan perhitungan bunga majemuk, dia dapat menghitung total tabungan yang dibutuhkan untuk membeli rumah.
Total tabungan = Nilai rumah + Bunga tabungan
Total tabungan = Rp500 juta + (Rp500 juta x 5% x 5 tahun)
Total tabungan = Rp500 juta + Rp125 juta
Total tabungan = Rp625 juta
Dengan demikian, karyawan tersebut perlu menabung minimal Rp625 juta selama 5 tahun untuk membeli rumah.
Pemungkas

Memahami konsep matematika tidak hanya penting untuk menyelesaikan soal ujian, tetapi juga untuk memahami dunia di sekitar kita. Dengan memahami konsep yang diuji dalam soal kelas 9 halaman 239 nomor 4, kamu akan dapat menyelesaikan berbagai masalah praktis yang melibatkan konsep tersebut.
Pertanyaan Umum yang Sering Muncul: Kunci Jawaban Matematika Kelas 9 Halaman 239 Nomor 4
Apakah soal ini berkaitan dengan persamaan linear?
Ya, soal ini kemungkinan besar berkaitan dengan persamaan linear atau sistem persamaan linear.
Apakah ada cara lain untuk menyelesaikan soal ini?
Ya, mungkin ada beberapa cara lain untuk menyelesaikan soal ini, tergantung pada konsep yang diuji.