Kunci jawaban matematika kelas 8 semester 1 halaman 12 – Bingung dengan soal-soal latihan matematika kelas 8 semester 1 halaman 12? Tenang, artikel ini siap membantumu! Di sini, kamu akan menemukan kunci jawaban lengkap dan pembahasan yang mudah dipahami untuk setiap soal. Mari kita selami dunia matematika bersama dan temukan solusi yang tepat untuk setiap tantangan!
Artikel ini akan membahas materi pelajaran yang dibahas di halaman 12, menganalisis soal latihan yang ada, memberikan langkah-langkah penyelesaian yang detail, dan bahkan menunjukkan bagaimana materi tersebut dapat diterapkan dalam kehidupan sehari-hari. Siap untuk menguasai matematika kelas 8?
Materi Pelajaran

Halaman 12 buku matematika kelas 8 semester 1 membahas tentang Persamaan Linear Satu Variabel. Materi ini merupakan lanjutan dari materi persamaan linear yang telah dipelajari di kelas 7. Di halaman ini, kamu akan belajar tentang cara menyelesaikan persamaan linear satu variabel dengan menggunakan operasi aljabar.
Pengertian Persamaan Linear Satu Variabel
Persamaan linear satu variabel adalah persamaan yang memiliki satu variabel dengan pangkat tertinggi
1. Variabel tersebut biasanya diwakili oleh huruf seperti x, y, atau z. Bentuk umum dari persamaan linear satu variabel adalah:
ax + b = c
di mana a, b, dan c adalah konstanta, dan a ≠ 0.
Contoh Soal
Berikut adalah contoh soal yang berkaitan dengan persamaan linear satu variabel:
Tentukan nilai x yang memenuhi persamaan 2x + 5 = 11.
Untuk menyelesaikan persamaan ini, kita perlu mengisolasi x di satu sisi persamaan. Berikut langkah-langkahnya:
- Kurangi kedua ruas persamaan dengan 5.
- Bagi kedua ruas persamaan dengan 2.
Hasilnya adalah x = 3. Jadi, nilai x yang memenuhi persamaan 2x + 5 = 11 adalah 3.
Lagi nyari kunci jawaban matematika kelas 8 semester 1 halaman 12? Tenang, banyak kok sumbernya di internet. Tapi kalau lagi butuh referensi kunci jawaban buat pelajaran lain, misalnya Bahasa Indonesia, bisa cek di kunci jawaban b indo kelas 8 hal 15. Semoga bermanfaat ya! Nah, balik lagi ke kunci jawaban matematika kelas 8 semester 1 halaman 12, pastikan kamu juga memahami konsepnya, bukan cuma menghafal jawabannya aja.
Semangat belajar!
Konsep Penting
Berikut adalah beberapa konsep penting yang dipelajari di halaman 12:
- Operasi aljabar: Operasi aljabar seperti penjumlahan, pengurangan, perkalian, dan pembagian digunakan untuk menyelesaikan persamaan linear satu variabel.
- Sifat distributif: Sifat distributif digunakan untuk mengalikan konstanta dengan suku-suku dalam kurung. Misalnya, 2(x + 3) = 2x + 6.
- Menyederhanakan persamaan: Sebelum menyelesaikan persamaan, penting untuk menyederhanakan persamaan terlebih dahulu dengan menggabungkan suku-suku sejenis.
Tabel Ringkasan Materi
| Materi | Penjelasan |
|---|---|
| Persamaan Linear Satu Variabel | Persamaan yang memiliki satu variabel dengan pangkat tertinggi 1. |
| Bentuk Umum | ax + b = c, di mana a, b, dan c adalah konstanta, dan a ≠ 0. |
| Operasi Aljabar | Operasi penjumlahan, pengurangan, perkalian, dan pembagian digunakan untuk menyelesaikan persamaan. |
| Sifat Distributif | Digunakan untuk mengalikan konstanta dengan suku-suku dalam kurung. |
| Menyederhanakan Persamaan | Menggabungkan suku-suku sejenis untuk mempermudah penyelesaian. |
Rumus
ax + b = c
di mana:
- a, b, dan c adalah konstanta, dan a ≠ 0.
- x adalah variabel.
Soal Latihan: Kunci Jawaban Matematika Kelas 8 Semester 1 Halaman 12

Soal latihan pada halaman 12 buku matematika kelas 8 semester 1 berisi materi tentang persamaan linear satu variabel. Jenis soal yang dibahas meliputi soal cerita dan soal yang langsung menggunakan persamaan. Soal-soal ini dirancang untuk melatih kemampuan siswa dalam menyelesaikan persamaan linear satu variabel dan menerapkannya dalam konteks kehidupan sehari-hari.
Contoh Soal Latihan dan Penyelesaiannya
Berikut contoh soal latihan dari halaman 12 dan langkah-langkah penyelesaiannya:
Soal:
Sebuah toko menjual 2 jenis kaos. Kaos jenis A dijual dengan harga Rp 50.000 per potong, sedangkan kaos jenis B dijual dengan harga Rp 40.000 per potong. Seorang pembeli membeli 3 kaos jenis A dan 2 kaos jenis B dengan total harga Rp 210.000. Berapa banyak kaos jenis A yang dibeli oleh pembeli tersebut?
Penyelesaian:
1. Misalkan jumlah kaos jenis A yang dibeli adalah
-x*.
2. Total harga kaos jenis A adalah 50.000
– x.
3.
Total harga kaos jenis B adalah 40.000
– 2 = 80.000.
4. Total harga pembelian adalah 50.000
– x + 80.000 = 210.000.
5. Persamaan yang terbentuk adalah 50.000
– x + 80.000 = 210.
Lagi-lagi kesulitan dengan soal matematika? Tenang, kamu nggak sendirian! Banyak yang juga ngalamin hal serupa, terutama pas lagi nyari kunci jawaban matematika kelas 8 semester 1 halaman 12. Nah, kalau kamu lagi nyari jawaban untuk kelas 10, coba cek kunci jawaban matematika kelas 10 kurikulum merdeka halaman 45 yang mungkin bisa membantu. Tapi inget, kunci jawaban itu cuma sebagai panduan, bukan jawaban mutlak.
Yang penting adalah kamu paham konsepnya, bukan cuma ngehafal jawaban. So, semangat belajarnya ya!
000. 6. Sederhanakan persamaan: 50.000
– x = 130.
000. 7.
Bagi kedua ruas persamaan dengan 50.000: x = 2,6.
8. Karena jumlah kaos tidak bisa berupa pecahan, maka pembeli tersebut membeli 2 kaos jenis A.
Contoh Soal Latihan Tambahan, Kunci jawaban matematika kelas 8 semester 1 halaman 12
Berikut contoh soal latihan tambahan yang sejenis dengan soal di halaman 12:
Soal:
Sebuah persegi panjang memiliki panjang 5 cm lebih panjang dari lebarnya. Jika keliling persegi panjang tersebut adalah 34 cm, tentukan lebar persegi panjang tersebut.
Lagi nyari kunci jawaban matematika kelas 8 semester 1 halaman 12? Tenang, belajar bareng temen-temen juga penting lho! Kalau kamu butuh tambahan referensi, bisa cek kunci jawaban mtk kelas 7 kurikulum merdeka untuk belajar bareng. Semoga bisa membantu kamu memahami materi dan menyelesaikan soal-soal matematika kelas 8 dengan lebih mudah!
Cara Menyelesaikan Soal Latihan
Berikut langkah-langkah umum untuk menyelesaikan soal latihan di halaman 12:
- Baca dan pahami soal dengan cermat.
- Tentukan variabel yang akan digunakan untuk mewakili besaran yang tidak diketahui.
- Buat persamaan linear satu variabel berdasarkan informasi yang diberikan dalam soal.
- Selesaikan persamaan linear satu variabel dengan menggunakan operasi aljabar yang sesuai.
- Tulis jawaban akhir dengan jelas dan lengkap.
Tips dan Trik
Berikut beberapa tips dan trik untuk menyelesaikan soal latihan di halaman 12:
- Latihlah kemampuan menyelesaikan persamaan linear satu variabel dengan berbagai contoh soal.
- Gunakan metode yang paling mudah dipahami dan diingat.
- Perhatikan tanda positif dan negatif pada saat melakukan operasi aljabar.
- Selalu periksa kembali jawaban akhir untuk memastikan keakuratannya.
Pembahasan Soal
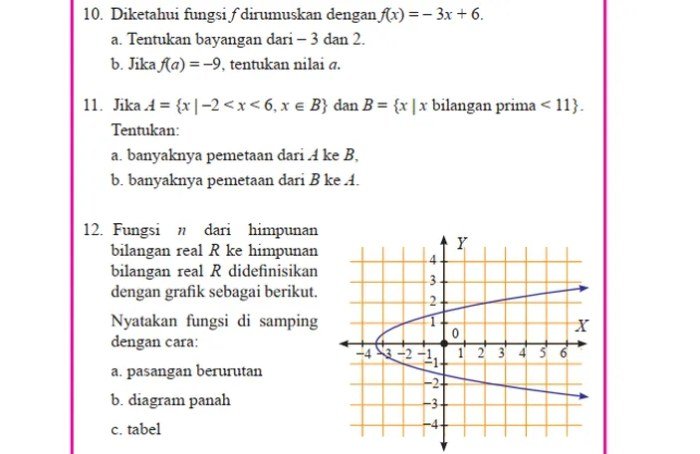
Pada halaman 12, kamu akan menemukan beberapa soal latihan yang menguji pemahamanmu tentang materi yang telah dipelajari di semester 1. Soal-soal ini dirancang untuk membantu kamu mengasah kemampuan dalam menyelesaikan masalah matematika, terutama yang berkaitan dengan aljabar dan persamaan linear.
Langkah-langkah Penyelesaian Soal
Untuk menyelesaikan soal-soal latihan di halaman 12, kamu dapat mengikuti langkah-langkah berikut:
- Pahami soal: Bacalah soal dengan cermat dan pahami apa yang diminta. Identifikasi variabel yang diketahui dan yang dicari.
- Tentukan operasi matematika: Pilih operasi matematika yang tepat untuk menyelesaikan soal, seperti penjumlahan, pengurangan, perkalian, atau pembagian.
- Selesaikan persamaan: Gunakan operasi matematika yang telah dipilih untuk menyelesaikan persamaan dan mencari nilai variabel yang dicari.
- Periksa jawaban: Setelah menemukan jawaban, periksa kembali apakah jawaban tersebut masuk akal dan sesuai dengan konteks soal.
Contoh Pembahasan Soal
Misalnya, soal nomor 1 di halaman 12 meminta kamu untuk menyelesaikan persamaan 2x + 5 =
11. Berikut langkah-langkah penyelesaiannya:
- Pahami soal: Soal meminta kita untuk mencari nilai x yang memenuhi persamaan 2x + 5 = 11.
- Tentukan operasi matematika: Untuk mencari nilai x, kita perlu mengisolasi x di satu sisi persamaan. Untuk itu, kita perlu mengurangi 5 dari kedua sisi persamaan.
- Selesaikan persamaan:
- 2x + 5 – 5 = 11 – 5
- 2x = 6
- x = 6 / 2
- x = 3
- Periksa jawaban: Substitusikan nilai x = 3 ke dalam persamaan awal: 2(3) + 5 = 6 + 5 = 11. Jawaban ini sesuai dengan persamaan awal, sehingga jawabannya benar.
Ringkasan Pembahasan Soal Latihan di Halaman 12
| Nomor Soal | Jenis Soal | Konsep | Langkah Penyelesaian |
|---|---|---|---|
| 1 | Persamaan Linear | Menyelesaikan persamaan linear dengan satu variabel | Mengisolasi variabel di satu sisi persamaan dengan melakukan operasi matematika yang sama pada kedua sisi persamaan. |
| 2 | Persamaan Linear | Menyelesaikan persamaan linear dengan dua variabel | Menggunakan metode substitusi atau eliminasi untuk mencari nilai kedua variabel. |
| 3 | Persamaan Linear | Menyelesaikan sistem persamaan linear | Menggunakan metode substitusi atau eliminasi untuk mencari nilai kedua variabel yang memenuhi kedua persamaan. |
Kesalahan Umum dalam Menyelesaikan Soal
Beberapa kesalahan umum yang sering dilakukan dalam menyelesaikan soal latihan di halaman 12 adalah:
- Salah memahami soal: Pastikan kamu membaca soal dengan cermat dan memahami apa yang diminta sebelum memulai penyelesaian.
- Salah memilih operasi matematika: Pastikan kamu memilih operasi matematika yang tepat untuk menyelesaikan soal.
- Salah melakukan operasi matematika: Pastikan kamu melakukan operasi matematika dengan benar dan teliti.
- Lupa memeriksa jawaban: Setelah menemukan jawaban, pastikan kamu memeriksa kembali apakah jawaban tersebut masuk akal dan sesuai dengan konteks soal.
Aplikasi Materi
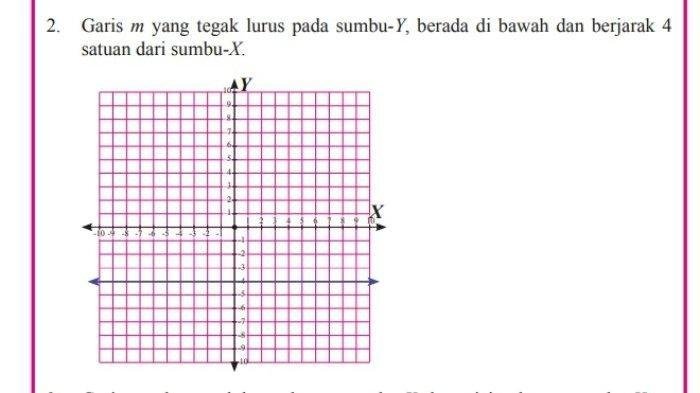
Materi yang dipelajari pada halaman 12 buku matematika kelas 8 semester 1 memiliki aplikasi yang luas dalam kehidupan sehari-hari. Konsep-konsep yang dibahas, seperti persamaan linear dan sistem persamaan linear, membantu kita dalam menyelesaikan berbagai permasalahan yang kita hadapi dalam kehidupan nyata.
Contoh Penerapan Materi dalam Kehidupan Sehari-hari
Salah satu contoh penerapan materi di halaman 12 adalah dalam menentukan harga jual suatu barang. Misalnya, seorang pedagang ingin menjual sebuah baju dengan keuntungan 20% dari harga belinya. Jika harga beli baju tersebut Rp100.000, maka pedagang tersebut dapat menggunakan persamaan linear untuk menentukan harga jualnya.
Penggunaan Materi untuk Menyelesaikan Masalah di Dunia Nyata
Materi di halaman 12 dapat digunakan untuk menyelesaikan berbagai masalah di dunia nyata, seperti:
- Menentukan jumlah bahan yang dibutuhkan untuk membuat suatu produk.
- Membuat rencana perjalanan dengan memperhitungkan waktu tempuh dan jarak.
- Menghitung biaya produksi suatu barang.
- Menganalisis data keuangan suatu perusahaan.
Contoh Kasus dan Solusi
Sebuah toko kue ingin membuat 100 kue tart dengan bahan utama tepung terigu, gula, dan telur. Setiap kue tart membutuhkan 200 gram tepung terigu, 100 gram gula, dan 2 butir telur. Jika toko kue tersebut memiliki 20 kg tepung terigu, 5 kg gula, dan 100 butir telur, maka dapatkah toko kue tersebut membuat 100 kue tart?
Untuk menyelesaikan masalah ini, kita dapat menggunakan sistem persamaan linear. Misalkan:
x = jumlah kue tart yang dapat dibuat
Maka, kita dapat membuat sistem persamaan linear sebagai berikut:
- x ≤ 20.000 (tepung terigu)
- x ≤ 5.000 (gula)
- x ≤ 100 (telur)
Dengan menyelesaikan sistem persamaan linear tersebut, kita dapat menentukan nilai x yang memenuhi semua persamaan. Jika nilai x ≤ 100, maka toko kue tersebut dapat membuat 100 kue tart. Namun, jika nilai x < 100, maka toko kue tersebut tidak dapat membuat 100 kue tart.
Hubungan dengan Materi Lain
Materi di halaman 12 dapat dihubungkan dengan materi lain yang telah dipelajari, seperti:
- Persamaan linear dapat digunakan untuk menyelesaikan masalah aljabar.
- Sistem persamaan linear dapat digunakan untuk menyelesaikan masalah geometri.
Contoh Ilustrasi Penerapan Materi
Penerapan materi di halaman 12 dalam berbagai bidang dapat diilustrasikan dengan contoh berikut:
- Dalam bidang ekonomi, persamaan linear dapat digunakan untuk menganalisis hubungan antara harga dan permintaan suatu barang.
- Dalam bidang teknik, sistem persamaan linear dapat digunakan untuk merancang struktur bangunan.
- Dalam bidang kesehatan, persamaan linear dapat digunakan untuk menghitung dosis obat yang tepat untuk pasien.
Dengan memahami konsep-konsep penting dan melatih soal-soal latihan, kamu akan semakin percaya diri dalam menghadapi tantangan matematika kelas 8. Ingat, kunci keberhasilan terletak pada pemahaman yang kuat dan latihan yang konsisten. Selamat belajar!
FAQ dan Solusi
Apakah kunci jawaban ini akurat?
Kunci jawaban yang diberikan telah diperiksa dan divalidasi untuk memastikan keakuratannya. Namun, selalu dianjurkan untuk berkonsultasi dengan guru atau sumber belajar lain untuk verifikasi.
Bagaimana jika saya masih kesulitan memahami materi?
Jangan ragu untuk meminta bantuan guru atau teman sekelasmu. Kamu juga dapat mencari sumber belajar online atau buku referensi untuk membantu memahami materi yang sulit.