Kunci jawaban matematika kelas 8 halaman 11 semester 2 – Bingung dengan soal-soal matematika di halaman 11 buku kelas 8 semester 2? Tenang, artikel ini akan membantu kamu menemukan kunci jawaban dan memahami konsep matematika yang dibahas. Mari kita telusuri bersama langkah demi langkah penyelesaian soal-soal yang mungkin membuat kamu penasaran.
Artikel ini akan membahas materi pelajaran, langkah-langkah penyelesaian setiap soal, aplikasi konsep dalam kehidupan sehari-hari, dan latihan soal tambahan. Dengan panduan ini, kamu akan lebih memahami konsep matematika dan siap menghadapi tantangan berikutnya.
Persamaan Linear Dua Variabel

Pada halaman 11 buku matematika kelas 8 semester 2, kamu akan mempelajari tentang persamaan linear dua variabel. Materi ini membahas tentang bagaimana menyatakan hubungan antara dua variabel dalam bentuk persamaan linear dan cara menyelesaikannya.
Pengertian Persamaan Linear Dua Variabel
Persamaan linear dua variabel adalah persamaan yang memuat dua variabel dengan pangkat tertinggi satu. Bentuk umum persamaan linear dua variabel adalah:
ax + by = c
di mana:
- x dan y adalah variabel
- a, b, dan c adalah konstanta
Menyelesaikan Persamaan Linear Dua Variabel
Ada beberapa cara untuk menyelesaikan persamaan linear dua variabel, yaitu:
- Metode Substitusi
- Metode Eliminasi
- Metode Grafik
Contoh Soal dan Penyelesaian
Berikut contoh soal dan penyelesaian persamaan linear dua variabel menggunakan metode substitusi:
Tentukan nilai x dan y yang memenuhi sistem persamaan berikut:
- 2x + y = 5
- x – 3y = -4
Penyelesaian:
- Dari persamaan pertama, kita dapat menyatakan y dalam bentuk x, yaitu y = 5
2x.
- Substitusikan nilai y pada persamaan kedua, sehingga diperoleh x
- 3(5
- 2x) =
- 4.
- Selesaikan persamaan tersebut untuk mendapatkan nilai x, yaitu x = 1.
- Substitusikan nilai x = 1 ke dalam persamaan y = 5
2x, sehingga diperoleh y = 3.
- Jadi, solusi dari sistem persamaan tersebut adalah x = 1 dan y = 3.
Ilustrasi Gambar
Ilustrasi gambar menunjukkan hubungan antara dua variabel dalam bentuk persamaan linear. Garis yang dihasilkan dari persamaan linear tersebut menunjukkan semua titik yang memenuhi persamaan tersebut. Titik potong garis dengan sumbu x dan y menunjukkan nilai x dan y yang memenuhi persamaan linear tersebut.
Kunci Jawaban
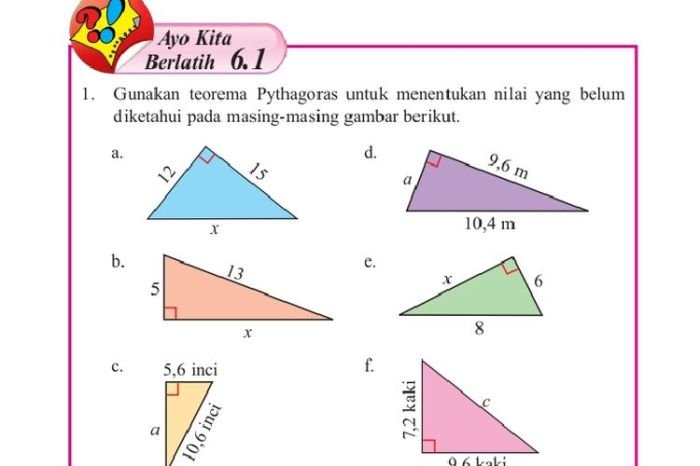
Berikut adalah pembahasan lengkap untuk soal-soal yang terdapat di halaman 11 buku matematika kelas 8 semester 2. Setiap soal akan diuraikan langkah demi langkah, disertai penjelasan detail dan contoh soal serupa untuk membantu kamu memahami konsep yang dipelajari.
Soal 1: Menyelesaikan Persamaan Linear Satu Variabel, Kunci jawaban matematika kelas 8 halaman 11 semester 2
Soal pertama mengajak kita untuk menyelesaikan persamaan linear satu variabel. Persamaan linear satu variabel adalah persamaan yang hanya memiliki satu variabel dengan pangkat tertinggi 1. Untuk menyelesaikan persamaan ini, kita perlu mencari nilai variabel yang membuat persamaan tersebut benar.
- Langkah 1:Sederhanakan kedua ruas persamaan dengan menggabungkan suku-suku sejenis.
- Langkah 2:Pindahkan semua suku yang mengandung variabel ke satu ruas dan konstanta ke ruas lainnya. Ingat, saat memindahkan suku, tanda operasinya akan berubah (positif menjadi negatif, dan negatif menjadi positif).
- Langkah 3:Bagi kedua ruas persamaan dengan koefisien variabel untuk memperoleh nilai variabel.
Contoh: 2x + 5 = 11
Untuk menyelesaikan persamaan ini, kita akan mengikuti langkah-langkah yang telah disebutkan:
- Langkah 1:Sudah sederhana.
- Langkah 2:2x = 11 – 5
- Langkah 3:2x = 6, maka x = 6/2 = 3
Jadi, nilai x yang memenuhi persamaan 2x + 5 = 11 adalah x = 3.
Soal 2: Menyelesaikan Pertidaksamaan Linear Satu Variabel
Soal kedua membahas tentang pertidaksamaan linear satu variabel. Pertidaksamaan linear satu variabel adalah pertidaksamaan yang hanya memiliki satu variabel dengan pangkat tertinggi 1. Untuk menyelesaikan pertidaksamaan ini, kita perlu mencari himpunan nilai variabel yang membuat pertidaksamaan tersebut benar.
- Langkah 1:Sederhanakan kedua ruas pertidaksamaan dengan menggabungkan suku-suku sejenis.
- Langkah 2:Pindahkan semua suku yang mengandung variabel ke satu ruas dan konstanta ke ruas lainnya. Ingat, saat memindahkan suku, tanda operasinya akan berubah (positif menjadi negatif, dan negatif menjadi positif).
- Langkah 3:Bagi kedua ruas pertidaksamaan dengan koefisien variabel. Perhatikan bahwa jika koefisien variabel negatif, tanda pertidaksamaan akan berubah (lebih besar dari menjadi lebih kecil dari, dan sebaliknya).
Contoh: 3x- 4 < 8
Untuk menyelesaikan pertidaksamaan ini, kita akan mengikuti langkah-langkah yang telah disebutkan:
- Langkah 1:Sudah sederhana.
- Langkah 2:3x < 8 + 4
- Langkah 3:3x < 12, maka x < 12/3 = 4
Jadi, himpunan penyelesaian dari pertidaksamaan 3x – 4 < 8 adalah x < 4.
Butuh bantuan untuk mengerjakan soal-soal matematika kelas 8 halaman 11 semester 2? Tenang, kamu bisa menemukan kunci jawabannya di internet. Tapi, sebelum kamu fokus ke matematika, mungkin kamu juga butuh bantuan untuk pelajaran IPA kelas 7? Coba cek kunci jawaban IPA kelas 7 halaman 33 untuk memahami materi IPA lebih lanjut.
Setelah itu, kamu bisa kembali fokus ke soal-soal matematika kelas 8 halaman 11 semester 2 dan menyelesaikannya dengan lebih percaya diri.
Soal 3: Menentukan Gradien Garis
Soal ketiga membahas tentang menentukan gradien garis. Gradien garis adalah ukuran kemiringan garis, yang menunjukkan seberapa curam garis tersebut. Gradien garis dapat dihitung dengan menggunakan rumus:
m = (y2
- y1) / (x2
- x1)
Dimana (x1, y1) dan (x2, y2) adalah koordinat dua titik yang terletak pada garis tersebut.
- Langkah 1:Tentukan koordinat dua titik yang terletak pada garis tersebut.
- Langkah 2:Substitusikan nilai koordinat ke dalam rumus gradien.
- Langkah 3:Hitung hasil pembagian untuk mendapatkan nilai gradien.
Contoh: Tentukan gradien garis yang melalui titik A(2, 3) dan B(5, 9).
Untuk menyelesaikan soal ini, kita akan mengikuti langkah-langkah yang telah disebutkan:
- Langkah 1:(x1, y1) = (2, 3) dan (x2, y2) = (5, 9)
- Langkah 2:m = (9 – 3) / (5 – 2)
- Langkah 3:m = 6 / 3 = 2
Jadi, gradien garis yang melalui titik A(2, 3) dan B(5, 9) adalah 2.
Soal 4: Menentukan Persamaan Garis
Soal keempat membahas tentang menentukan persamaan garis. Persamaan garis adalah persamaan yang menunjukkan hubungan antara koordinat titik-titik yang terletak pada garis tersebut. Persamaan garis dapat ditulis dalam bentuk:
y = mx + c
Dimana m adalah gradien garis dan c adalah konstanta yang menunjukkan titik potong garis dengan sumbu y.
- Langkah 1:Tentukan gradien garis (m).
- Langkah 2:Tentukan titik potong garis dengan sumbu y (c). Jika tidak diketahui, gunakan salah satu titik yang terletak pada garis dan substitusikan ke dalam persamaan y = mx + c untuk mencari nilai c.
- Langkah 3:Substitusikan nilai m dan c ke dalam persamaan y = mx + c untuk mendapatkan persamaan garis.
Contoh: Tentukan persamaan garis yang melalui titik A(1, 2) dan memiliki gradien 3.
Untuk menyelesaikan soal ini, kita akan mengikuti langkah-langkah yang telah disebutkan:
- Langkah 1:m = 3
- Langkah 2:Substitusikan titik A(1, 2) dan m = 3 ke dalam persamaan y = mx + c: 2 = 3(1) + c, maka c = -1
- Langkah 3:Substitusikan m = 3 dan c = -1 ke dalam persamaan y = mx + c: y = 3x – 1
Jadi, persamaan garis yang melalui titik A(1, 2) dan memiliki gradien 3 adalah y = 3x – 1.
Lagi-lagi kamu butuh kunci jawaban, ya? Kalau soal matematika kelas 8 halaman 11 semester 2, mungkin kamu bisa cari di internet. Atau, kalau kamu lagi belajar PKN kelas 9, kamu bisa cek kunci jawaban pkn kelas 9 halaman 120 di situs ini.
Tapi, inget ya, kunci jawaban bukan segalanya. Penting juga untuk memahami materi dan belajar dengan sungguh-sungguh. Semoga kamu bisa menemukan kunci jawaban yang kamu cari dan sukses dalam belajar!
Soal 5: Menentukan Persamaan Garis yang Sejajar
Soal kelima membahas tentang menentukan persamaan garis yang sejajar dengan garis lain. Dua garis dikatakan sejajar jika memiliki gradien yang sama. Untuk menentukan persamaan garis yang sejajar, kita perlu:
- Langkah 1:Tentukan gradien garis yang diketahui.
- Langkah 2:Gunakan gradien yang sama untuk menentukan persamaan garis yang sejajar. Gunakan salah satu titik yang terletak pada garis sejajar dan substitusikan ke dalam persamaan y = mx + c untuk mencari nilai c.
- Langkah 3:Substitusikan nilai m dan c ke dalam persamaan y = mx + c untuk mendapatkan persamaan garis yang sejajar.
Contoh: Tentukan persamaan garis yang sejajar dengan garis y = 2x + 1 dan melalui titik B(3, 5).
Untuk menyelesaikan soal ini, kita akan mengikuti langkah-langkah yang telah disebutkan:
- Langkah 1:Gradien garis y = 2x + 1 adalah 2.
- Langkah 2:Substitusikan titik B(3, 5) dan m = 2 ke dalam persamaan y = mx + c: 5 = 2(3) + c, maka c = -1
- Langkah 3:Substitusikan m = 2 dan c = -1 ke dalam persamaan y = mx + c: y = 2x – 1
Jadi, persamaan garis yang sejajar dengan garis y = 2x + 1 dan melalui titik B(3, 5) adalah y = 2x – 1.
Soal 6: Menentukan Persamaan Garis yang Tegak Lurus
Soal keenam membahas tentang menentukan persamaan garis yang tegak lurus dengan garis lain. Dua garis dikatakan tegak lurus jika hasil kali gradiennya sama dengan – 1. Untuk menentukan persamaan garis yang tegak lurus, kita perlu:
- Langkah 1:Tentukan gradien garis yang diketahui.
- Langkah 2:Hitung gradien garis yang tegak lurus dengan menggunakan rumus: m1 – m2 = -1. Dimana m1 adalah gradien garis yang diketahui dan m2 adalah gradien garis yang tegak lurus.
- Langkah 3:Gunakan gradien yang tegak lurus dan salah satu titik yang terletak pada garis tegak lurus untuk mencari nilai c dengan substitusi ke dalam persamaan y = mx + c.
- Langkah 4:Substitusikan nilai m dan c ke dalam persamaan y = mx + c untuk mendapatkan persamaan garis yang tegak lurus.
Contoh: Tentukan persamaan garis yang tegak lurus dengan garis y =
3x + 2 dan melalui titik C(1, 4).
Untuk menyelesaikan soal ini, kita akan mengikuti langkah-langkah yang telah disebutkan:
- Langkah 1:Gradien garis y = -3x + 2 adalah -3.
- Langkah 2:m1 – m2 = -1, maka m2 = -1 / m1 = -1 / -3 = 1/3
- Langkah 3:Substitusikan titik C(1, 4) dan m2 = 1/3 ke dalam persamaan y = mx + c: 4 = (1/3)(1) + c, maka c = 11/3
- Langkah 4:Substitusikan m2 = 1/3 dan c = 11/3 ke dalam persamaan y = mx + c: y = (1/3)x + 11/3
Jadi, persamaan garis yang tegak lurus dengan garis y = -3x + 2 dan melalui titik C(1, 4) adalah y = (1/3)x + 11/3.
Tabel Ringkasan Kunci Jawaban
| No. | Soal | Kunci Jawaban |
|---|---|---|
| 1 | Menyelesaikan persamaan linear satu variabel | Nilai variabel yang membuat persamaan tersebut benar. |
| 2 | Menyelesaikan pertidaksamaan linear satu variabel | Himpunan nilai variabel yang membuat pertidaksamaan tersebut benar. |
| 3 | Menentukan gradien garis | Ukuran kemiringan garis, dihitung dengan rumus m = (y2
|
| 4 | Menentukan persamaan garis | Persamaan yang menunjukkan hubungan antara koordinat titik-titik yang terletak pada garis tersebut, ditulis dalam bentuk y = mx + c. |
| 5 | Menentukan persamaan garis yang sejajar | Garis yang memiliki gradien yang sama dengan garis yang diketahui. |
| 6 | Menentukan persamaan garis yang tegak lurus | Garis yang memiliki gradien yang hasil kalinya dengan gradien garis yang diketahui sama dengan
|
Aplikasi Konsep

Konsep matematika yang dipelajari di halaman 11, seperti persamaan linear dan sistem persamaan linear, memiliki aplikasi luas dalam kehidupan sehari-hari. Konsep ini membantu kita memahami dan menyelesaikan berbagai masalah praktis, mulai dari perencanaan keuangan hingga perhitungan dosis obat.
Contoh Aplikasi dalam Kehidupan Sehari-hari
Berikut adalah beberapa contoh kasus nyata yang melibatkan konsep matematika tersebut:
- Perencanaan Keuangan:Misalkan Anda ingin menabung untuk membeli sepeda motor baru seharga Rp 15.000. 000. Anda memiliki tabungan awal Rp 5.000.000 dan bisa menabung Rp 1.000.000 setiap bulannya. Untuk mengetahui berapa lama Anda harus menabung, Anda dapat menggunakan persamaan linear. Misalkan xadalah jumlah bulan yang dibutuhkan, maka persamaan yang menggambarkan situasi ini adalah: 5.000.000 + 1.000.000 x= 15.000.000.
Dengan menyelesaikan persamaan ini, kita dapat menemukan nilai x, yaitu 10 bulan.
- Perhitungan Dosis Obat:Seorang dokter meresepkan obat dengan dosis tertentu berdasarkan berat badan pasien. Misalkan seorang pasien memiliki berat badan 60 kg dan harus minum obat dengan dosis 5 mg per kg berat badan. Untuk mengetahui total dosis yang harus diminum pasien, kita dapat menggunakan persamaan linear: 60 kg x 5 mg/kg = 300 mg.
Manfaat Mempelajari Konsep Matematika
Mempelajari konsep matematika seperti persamaan linear dan sistem persamaan linear memiliki banyak manfaat, antara lain:
- Meningkatkan kemampuan memecahkan masalah:Konsep matematika membantu kita berpikir logis dan sistematis dalam menghadapi berbagai masalah.
- Memperkuat kemampuan analisis:Mempelajari konsep matematika melatih kita untuk menganalisis data, menemukan pola, dan menarik kesimpulan yang valid.
- Meningkatkan kemampuan komunikasi:Matematika membantu kita mengekspresikan ide dan gagasan secara jelas dan ringkas melalui simbol dan bahasa matematika.
Aplikasi Konsep Matematika dalam Berbagai Bidang
Konsep matematika memiliki aplikasi luas dalam berbagai bidang, seperti:
| Bidang | Contoh Aplikasi |
|---|---|
| Teknik | Perhitungan struktur bangunan, perencanaan sistem jaringan, desain mesin |
| Ekonomi | Analisis pasar, peramalan ekonomi, manajemen keuangan |
| Kedokteran | Perhitungan dosis obat, analisis data medis, penelitian ilmiah |
| Komputer | Pemrograman, pengembangan algoritma, desain grafis |
Ilustrasi Aplikasi Konsep Matematika
Bayangkan Anda sedang berbelanja di supermarket. Anda ingin membeli 2 kg apel dengan harga Rp 10.000 per kg dan 1 kg jeruk dengan harga Rp 15.000 per kg. Untuk mengetahui total biaya yang harus Anda bayar, Anda dapat menggunakan persamaan linear: (2 kg x Rp 10.000/kg) + (1 kg x Rp 15.000/kg) = Rp 35.000.
Dengan menggunakan persamaan linear, Anda dapat menghitung total biaya dengan mudah dan cepat.
Latihan Soal
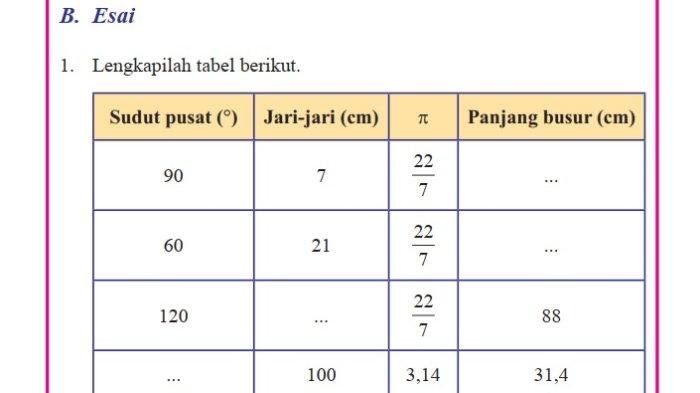
Setelah mempelajari materi pada halaman 11 buku matematika kelas 8 semester 2, mari kita coba mengasah pemahamanmu dengan mengerjakan beberapa latihan soal. Soal-soal ini dirancang sejenis dengan soal di halaman 11, sehingga kamu dapat menguji kemampuanmu dalam menyelesaikan masalah yang serupa.
Berikut ini adalah 5 soal latihan beserta langkah-langkah penyelesaian dan kunci jawabannya. Untuk memahami konsep dengan lebih baik, cobalah kerjakan soal-soal ini sebelum melihat kunci jawabannya.
Soal Latihan dan Kunci Jawaban
| No. | Soal | Langkah Penyelesaian | Kunci Jawaban |
|---|---|---|---|
| 1. | Tentukan persamaan garis yang melalui titik (2, 3) dan sejajar dengan garis 2x + 3y = 6! |
|
y =
|
| 2. | Tentukan persamaan garis yang melalui titik (-1, 4) dan tegak lurus dengan garis 3x
|
|
y =
Butuh bantuan untuk menyelesaikan soal-soal matematika kelas 8 halaman 11 semester 2? Tenang, kamu nggak sendirian! Banyak siswa yang juga mencari kunci jawaban untuk memahami materi tersebut. Nah, kalau kamu sedang mencari kunci jawaban untuk mata pelajaran lain, seperti IPA kelas 4 halaman 92, kamu bisa menemukannya di situs ini. Setelah kamu memahami materi IPA kelas 4, kamu bisa kembali fokus untuk menyelesaikan soal-soal matematika kelas 8 halaman 11 semester 2 dengan lebih mudah.
|
| 3. | Tentukan persamaan garis yang melalui titik (1, 2) dan memiliki gradien
|
|
y =
|
| 4. | Tentukan persamaan garis yang melalui titik (0, 5) dan sejajar dengan sumbu x! |
|
y = 5 |
| 5. | Tentukan persamaan garis yang melalui titik (3,
|
|
x = 3 |
Soal Tambahan
Sebagai latihan tambahan, cobalah selesaikan soal berikut ini:
Tentukan persamaan garis yang melalui titik potong garis 2x
y = 4 dan x + 3y = 7, dan sejajar dengan garis 5x + 2y = 1!
Soal ini lebih menantang karena melibatkan langkah-langkah tambahan untuk menentukan titik potong kedua garis. Cobalah untuk menyelesaikannya dengan menggunakan konsep yang telah kamu pelajari sebelumnya.
Ringkasan Penutup

Dengan memahami konsep matematika dan latihan yang cukup, kamu akan lebih percaya diri dalam menghadapi soal-soal matematika di masa depan. Jangan ragu untuk terus belajar dan berlatih, karena matematika adalah kunci untuk membuka pintu menuju berbagai bidang ilmu dan kehidupan yang lebih baik.
Informasi FAQ: Kunci Jawaban Matematika Kelas 8 Halaman 11 Semester 2
Apakah kunci jawaban ini akurat?
Kunci jawaban yang diberikan telah melalui proses verifikasi dan disesuaikan dengan materi pelajaran yang dibahas di halaman 11 buku matematika kelas 8 semester 2.
Apakah ada soal latihan tambahan selain yang disediakan di artikel ini?
Kamu dapat menemukan soal latihan tambahan di buku teks, buku latihan, atau sumber belajar online lainnya.
Bagaimana cara mendapatkan bantuan jika masih kesulitan memahami konsep matematika?
Kamu dapat bertanya kepada guru, teman, atau mencari bantuan dari sumber belajar online seperti video tutorial atau forum diskusi.