Bingung dengan soal matematika kelas 8 halaman 10 Kurikulum Merdeka? Tenang, kamu tidak sendirian! Banyak siswa yang merasa kesulitan memahami materi di halaman tersebut. Artikel ini akan membahas kunci jawaban matematika kelas 8 halaman 10 Kurikulum Merdeka secara detail, mulai dari memahami konsep, rumus, dan contoh soal yang dibahas.
Dengan memahami materi dan contoh soal yang diberikan, kamu akan lebih mudah menyelesaikan soal latihan dan memahami konsep matematika yang dipelajari. Yuk, simak penjelasan lengkapnya di bawah ini!
Memahami Kurikulum Merdeka
Kurikulum Merdeka merupakan kurikulum yang diterapkan di Indonesia untuk meningkatkan kualitas pendidikan dan relevansi dengan kebutuhan masa depan. Kurikulum ini hadir dengan berbagai perubahan signifikan dibandingkan dengan kurikulum sebelumnya.
Lagi-lagi kamu butuh bantuan kunci jawaban, ya? Kali ini untuk Matematika kelas 8 halaman 10 kurikulum merdeka? Tenang, banyak sumber yang bisa kamu gunakan. Oh, iya, kalau kamu butuh kunci jawaban IPA kelas 9 halaman 16, kamu bisa cek di situs ini.
Semoga membantu, ya! Nah, balik lagi ke kunci jawaban Matematika kelas 8 halaman 10, pastikan kamu memahami konsepnya, bukan hanya menghafal jawaban. Belajar yang rajin, ya!
Perbedaan Kurikulum Merdeka dengan Kurikulum Sebelumnya
Kurikulum Merdeka memiliki beberapa perbedaan utama dengan kurikulum sebelumnya, seperti Kurikulum 2013.
- Kurikulum Merdeka lebih fleksibel dan memberikan keleluasaan kepada guru dalam memilih dan mengatur materi pembelajaran. Guru dapat menyesuaikan materi dengan kebutuhan dan karakteristik siswa.
- Kurikulum Merdeka menekankan pada pembelajaran yang berpusat pada siswa, di mana siswa aktif dalam proses pembelajaran dan mengembangkan kemampuan berpikir kritis, kreatif, dan kolaboratif.
- Kurikulum Merdeka juga mengintegrasikan teknologi dalam pembelajaran, sehingga siswa dapat mengakses informasi dan sumber belajar yang lebih beragam.
Tujuan dan Manfaat Kurikulum Merdeka dalam Pembelajaran Matematika
Kurikulum Merdeka bertujuan untuk meningkatkan kualitas pembelajaran matematika dan membantu siswa mengembangkan kemampuan berpikir logis, analitis, dan sistematis.
- Kurikulum Merdeka memberikan ruang bagi siswa untuk belajar matematika secara lebih mendalam dan bermakna, sehingga dapat diterapkan dalam kehidupan sehari-hari.
- Kurikulum Merdeka mendorong siswa untuk aktif dalam proses pembelajaran, sehingga mereka lebih termotivasi dan memahami konsep matematika dengan lebih baik.
- Kurikulum Merdeka juga membantu guru dalam mengembangkan metode pembelajaran yang inovatif dan efektif, sehingga dapat meningkatkan hasil belajar siswa.
Contoh Materi Matematika Kelas 8 yang Dipelajari dalam Kurikulum Merdeka
Dalam Kurikulum Merdeka, materi matematika kelas 8 mencakup berbagai topik, seperti:
- Bilangan bulat dan operasi hitung
- Persamaan dan pertidaksamaan linear satu variabel
- Sistem persamaan linear dua variabel
- Persamaan garis lurus
- Segitiga dan segiempat
- Statistika
- Peluang
Materi-materi tersebut disajikan dengan pendekatan yang lebih kontekstual dan aplikatif, sehingga siswa dapat memahami konsep matematika dengan lebih mudah dan dapat menerapkannya dalam kehidupan sehari-hari.
Materi Matematika Kelas 8 Halaman 10
Halaman 10 buku matematika kelas 8 Kurikulum Merdeka membahas tentang persamaan linear satu variabel. Persamaan linear satu variabel adalah persamaan yang hanya memiliki satu variabel dengan pangkat tertinggi satu. Materi ini merupakan dasar untuk memahami konsep persamaan linear dan sistem persamaan linear yang akan dipelajari di tingkat selanjutnya.
Pengertian Persamaan Linear Satu Variabel
Persamaan linear satu variabel adalah persamaan yang hanya memiliki satu variabel dengan pangkat tertinggi satu. Variabel tersebut biasanya diwakili oleh huruf seperti x, y, atau z. Persamaan ini dapat ditulis dalam bentuk umum:
ax + b = 0
di mana:
- a dan b adalah konstanta (bilangan real)
- x adalah variabel
Contoh persamaan linear satu variabel:
- 2x + 5 = 0
- 3y – 7 = 1
- -4z + 2 = 8
Menyelesaikan Persamaan Linear Satu Variabel
Untuk menyelesaikan persamaan linear satu variabel, kita perlu mencari nilai variabel yang membuat persamaan tersebut benar. Ada beberapa metode yang dapat digunakan untuk menyelesaikan persamaan linear satu variabel, yaitu:
- Metode isolasi
- Metode substitusi
- Metode eliminasi
Metode Isolasi
Metode isolasi adalah metode yang paling umum digunakan untuk menyelesaikan persamaan linear satu variabel. Metode ini melibatkan manipulasi aljabar untuk mengisolasi variabel di satu sisi persamaan. Berikut adalah langkah-langkah untuk menyelesaikan persamaan linear satu variabel menggunakan metode isolasi:
- Sederhanakan persamaan dengan menggabungkan suku-suku sejenis.
- Pindahkan semua suku yang mengandung variabel ke satu sisi persamaan dan konstanta ke sisi lainnya.
- Bagi kedua sisi persamaan dengan koefisien variabel.
Contoh:
Selesaikan persamaan 2x + 5 = 0.
- 2x + 5 = 0
- 2x =
5
- x =
5/2
Jadi, solusi dari persamaan 2x + 5 = 0 adalah x = -5/2.
Butuh bantuan untuk menyelesaikan soal-soal matematika kelas 8 halaman 10 kurikulum merdeka? Tenang, kamu tidak sendirian! Banyak siswa yang juga merasa kesulitan dengan beberapa soal di buku tersebut. Nah, kalau kamu sedang mencari kunci jawaban untuk mata pelajaran lain, seperti Bahasa Indonesia misalnya, kamu bisa cek kunci jawaban bahasa indonesia kelas 9 halaman 38.
Website tersebut mungkin juga punya koleksi kunci jawaban untuk mata pelajaran lain, termasuk matematika. Semoga dengan bantuan ini, kamu bisa memahami materi dan menyelesaikan tugas-tugasmu dengan lebih mudah!
Metode Substitusi
Metode substitusi adalah metode yang digunakan untuk menyelesaikan sistem persamaan linear. Metode ini melibatkan penggantian nilai satu variabel dari satu persamaan ke persamaan lainnya. Berikut adalah langkah-langkah untuk menyelesaikan persamaan linear satu variabel menggunakan metode substitusi:
- Selesaikan salah satu persamaan untuk salah satu variabel.
- Substitusikan nilai variabel tersebut ke persamaan lainnya.
- Selesaikan persamaan yang baru terbentuk.
- Substitusikan nilai variabel yang telah ditemukan ke persamaan awal untuk menemukan nilai variabel lainnya.
Contoh:
Selesaikan sistem persamaan berikut:
- x + y = 5
- 2x – y = 1
- Selesaikan persamaan pertama untuk x: x = 5
y
- Substitusikan nilai x ke persamaan kedua: 2(5
- y)
- y = 1
- Selesaikan persamaan yang baru terbentuk: 10
- 2y
- y = 1, sehingga y = 3
- Substitusikan nilai y = 3 ke persamaan pertama: x + 3 = 5, sehingga x = 2
Jadi, solusi dari sistem persamaan tersebut adalah x = 2 dan y = 3.
Metode Eliminasi
Metode eliminasi adalah metode yang digunakan untuk menyelesaikan sistem persamaan linear. Metode ini melibatkan penghapusan salah satu variabel dengan cara menjumlahkan atau mengurangkan kedua persamaan. Berikut adalah langkah-langkah untuk menyelesaikan persamaan linear satu variabel menggunakan metode eliminasi:
- Kalikan kedua persamaan dengan konstanta sehingga koefisien variabel yang ingin dihilangkan sama.
- Jumlahkan atau kurangkan kedua persamaan.
- Selesaikan persamaan yang baru terbentuk.
- Substitusikan nilai variabel yang telah ditemukan ke persamaan awal untuk menemukan nilai variabel lainnya.
Contoh:
Selesaikan sistem persamaan berikut:
- x + y = 5
- 2x – y = 1
- Kalikan persamaan pertama dengan 2: 2x + 2y = 10
- Jumlahkan kedua persamaan: 4x = 11
- Selesaikan persamaan yang baru terbentuk: x = 11/4
- Substitusikan nilai x = 11/4 ke persamaan pertama: 11/4 + y = 5, sehingga y = 9/4
Jadi, solusi dari sistem persamaan tersebut adalah x = 11/4 dan y = 9/4.
Contoh Soal Latihan
Berikut adalah beberapa contoh soal latihan yang relevan dengan materi halaman 10:
- Selesaikan persamaan linear 3x
7 = 10.
- Tentukan nilai x yang memenuhi persamaan 2(x
3) = 5x + 1.
- Selesaikan sistem persamaan berikut:
- x + 2y = 7
- 3x – y = 1
Menyusun Tabel Rangkuman
Membuat tabel rangkuman adalah cara efektif untuk memahami materi pelajaran dengan lebih mudah. Tabel rangkuman membantu kita untuk melihat hubungan antara konsep, rumus, dan contoh soal dalam satu tampilan yang terstruktur.
Materi Halaman 10
Tabel rangkuman berikut ini berisi topik, konsep, rumus, dan contoh soal yang terdapat pada halaman 10 buku matematika kelas 8 kurikulum merdeka.
| Topik | Konsep | Rumus | Contoh Soal |
|---|---|---|---|
| Persamaan Linear Satu Variabel | Persamaan linear satu variabel adalah persamaan yang memiliki satu variabel dengan pangkat tertinggi 1. | ax + b = c, dengan a, b, dan c adalah konstanta dan a ≠ 0. | Tentukan nilai x yang memenuhi persamaan 2x + 5 = 11. |
| Penyelesaian Persamaan Linear Satu Variabel | Penyelesaian persamaan linear satu variabel dilakukan dengan mencari nilai variabel yang membuat persamaan tersebut benar. | – Menggabungkan suku-suku sejenis.
Butuh bantuan untuk menyelesaikan soal matematika kelas 8 halaman 10 kurikulum merdeka? Tenang, banyak sumber yang bisa kamu akses, termasuk kunci jawabannya. Tapi, kalau kamu sedang butuh referensi untuk mata pelajaran lain, seperti bahasa Indonesia, kamu bisa coba cek kunci jawaban bahasa Indonesia kelas 9 halaman 21. Nah, setelah kamu selesai belajar bahasa Indonesia, kamu bisa kembali fokus ke soal matematika kelas 8 halaman 10 kurikulum merdeka dan coba kerjakan lagi dengan lebih percaya diri!
|
Selesaikan persamaan 3x
|
Penerapan Konsep dalam Kehidupan Sehari-hari

Konsep matematika yang dipelajari di halaman 10, seperti persamaan linear, memiliki aplikasi yang luas dalam kehidupan sehari-hari. Konsep ini membantu kita memahami dan menyelesaikan berbagai masalah yang kita hadapi, mulai dari menghitung biaya hingga merencanakan perjalanan.
Contoh Penerapan Persamaan Linear
Bayangkan kamu ingin membeli beberapa buku tulis dan pensil. Setiap buku tulis harganya Rp5.000 dan setiap pensil harganya Rp1.000. Kamu ingin membeli 3 buku tulis dan beberapa pensil, dan kamu memiliki uang Rp20.000. Berapa banyak pensil yang bisa kamu beli?
Kita dapat menggunakan persamaan linear untuk menyelesaikan masalah ini. Misalkan x adalah jumlah pensil yang dapat kamu beli. Persamaan linearnya adalah:
5.000
- 3 + 1.000
- x = 20.000
Dengan menyelesaikan persamaan ini, kita mendapatkan:
x = 5
Jadi, kamu dapat membeli 5 pensil.
Manfaat Mempelajari Persamaan Linear
Mempelajari persamaan linear memiliki beberapa manfaat, antara lain:
- Meningkatkan kemampuan berpikir logis dan analitis.
- Membantu dalam menyelesaikan masalah sehari-hari, seperti perencanaan anggaran, menghitung jarak, dan menentukan kecepatan.
- Membuka peluang untuk mempelajari konsep matematika yang lebih kompleks di masa depan.
Ilustrasi Penerapan Persamaan Linear
Contoh lain penerapan persamaan linear adalah dalam menghitung jarak tempuh. Misalkan kamu ingin melakukan perjalanan dari kota A ke kota B dengan kecepatan 60 km/jam. Jika jarak antara kota A dan kota B adalah 300 km, berapa lama waktu yang dibutuhkan untuk sampai ke kota B?
Kita dapat menggunakan persamaan linear untuk menghitung waktu tempuh. Misalkan t adalah waktu tempuh dalam jam. Persamaan linearnya adalah:
60
t = 300
Dengan menyelesaikan persamaan ini, kita mendapatkan:
t = 5
Jadi, waktu yang dibutuhkan untuk sampai ke kota B adalah 5 jam.
Pembahasan Soal Latihan: Kunci Jawaban Matematika Kelas 8 Halaman 10 Kurikulum Merdeka

Soal-soal latihan pada halaman 10 buku Matematika kelas 8 Kurikulum Merdeka dirancang untuk membantu kamu memahami konsep-konsep yang telah dipelajari. Mari kita bahas tiga soal latihan yang dipilih secara acak dan pelajari langkah-langkah penyelesaiannya.
Soal Latihan 1: Menentukan Suku Ke-n Barisan Aritmatika
Soal latihan pertama membahas tentang barisan aritmatika. Dalam soal ini, kita diminta untuk menentukan suku ke-n dari suatu barisan aritmatika. Barisan aritmatika adalah barisan bilangan yang memiliki selisih yang sama antara dua suku yang berurutan. Selisih ini disebut dengan beda (b).
Rumus umum untuk menentukan suku ke-n (Un) dari barisan aritmatika adalah:
Un = a + (n
1) b
Dimana:
- Un = Suku ke-n
- a = Suku pertama
- b = Beda
- n = Nomor urut suku
Untuk menyelesaikan soal ini, kita perlu mengidentifikasi suku pertama (a), beda (b), dan nomor urut suku (n) yang ingin kita cari. Setelah itu, kita dapat memasukkan nilai-nilai tersebut ke dalam rumus Un.
Soal Latihan 2: Menyelesaikan Persamaan Linear Satu Variabel
Soal latihan kedua berkaitan dengan persamaan linear satu variabel. Persamaan linear satu variabel adalah persamaan yang hanya memiliki satu variabel dan pangkat tertinggi dari variabel tersebut adalah satu. Untuk menyelesaikan persamaan linear satu variabel, kita perlu mencari nilai variabel yang membuat persamaan tersebut benar.
Langkah-langkah umum untuk menyelesaikan persamaan linear satu variabel adalah:
- Sederhanakan kedua ruas persamaan dengan menggabungkan suku-suku sejenis.
- Pindahkan semua suku yang mengandung variabel ke satu ruas dan suku konstanta ke ruas lainnya.
- Bagi kedua ruas persamaan dengan koefisien variabel.
Dengan mengikuti langkah-langkah tersebut, kita akan mendapatkan nilai variabel yang memenuhi persamaan.
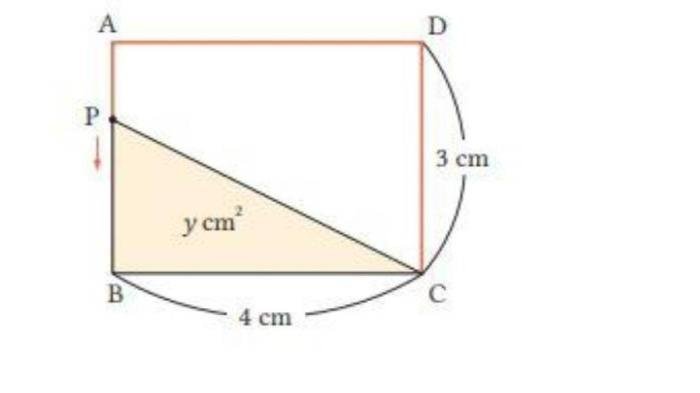
Soal Latihan 3: Menghitung Luas Segitiga, Kunci jawaban matematika kelas 8 halaman 10 kurikulum merdeka
Soal latihan ketiga membahas tentang menghitung luas segitiga. Luas segitiga adalah ukuran area yang dibentuk oleh segitiga. Rumus umum untuk menghitung luas segitiga adalah:
Luas = 1/2 x alas x tinggi
Dimana:
- Alas = Panjang sisi alas segitiga
- Tinggi = Jarak tegak lurus dari puncak segitiga ke alas
Untuk menyelesaikan soal ini, kita perlu mengidentifikasi panjang alas dan tinggi segitiga. Setelah itu, kita dapat memasukkan nilai-nilai tersebut ke dalam rumus luas segitiga.
Kesimpulan Akhir

Dengan memahami konsep matematika yang dipelajari di halaman 10 Kurikulum Merdeka, kamu akan lebih mudah menyelesaikan soal latihan dan menerapkannya dalam kehidupan sehari-hari. Jangan lupa untuk berlatih dan memahami setiap konsep dengan baik. Selamat belajar!
Pertanyaan yang Sering Diajukan
Apakah kunci jawaban ini sesuai dengan Kurikulum Merdeka?
Ya, kunci jawaban ini disusun berdasarkan materi matematika kelas 8 halaman 10 Kurikulum Merdeka.
Bagaimana cara mendapatkan kunci jawaban lengkap?
Kunci jawaban lengkap dapat diakses melalui website resmi Kemdikbud atau buku panduan guru Kurikulum Merdeka.
Apakah ada video pembelajaran untuk materi ini?
Ya, kamu dapat menemukan video pembelajaran di platform online seperti YouTube atau Ruangguru.