Sedang mencari kunci jawaban matematika kelas 9 halaman 180? Tenang, kamu tidak sendirian! Banyak siswa yang merasa kesulitan memahami materi dan menyelesaikan soal-soal di halaman tersebut. Namun, jangan khawatir, artikel ini akan membantumu memahami konsep-konsep penting dan langkah-langkah penyelesaian soal yang ada di halaman 180 buku matematika kelas 9.
Kita akan menjelajahi materi yang dibahas, menganalisis jenis soal, dan merangkum konsep-konsep penting yang terkait. Selain itu, kita juga akan membahas bagaimana materi ini dapat diterapkan dalam kehidupan sehari-hari dan memberikan tips dan trik untuk menguasai materi ini dengan mudah.
Latar Belakang: Kunci Jawaban Matematika Kelas 9 Halaman 180
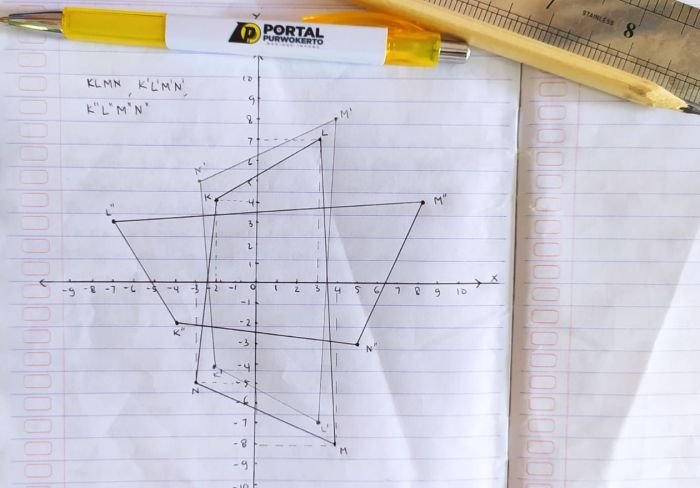
Pada halaman 180 buku pelajaran matematika kelas 9, kita akan membahas tentang persamaan garis lurus. Persamaan garis lurus merupakan konsep dasar dalam matematika yang penting untuk memahami hubungan antara dua variabel.
Pengertian Persamaan Garis Lurus
Persamaan garis lurus adalah sebuah rumus matematika yang menggambarkan hubungan antara dua variabel, biasanya x dan y, yang membentuk garis lurus pada bidang kartesius. Persamaan ini menunjukkan bagaimana nilai y berubah seiring perubahan nilai x.
Bentuk Umum Persamaan Garis Lurus
Bentuk umum persamaan garis lurus adalah:
y = mx + c
di mana:* y adalah nilai variabel y
- x adalah nilai variabel x
- m adalah gradien garis, yang menunjukkan kemiringan garis
- c adalah konstanta, yang menunjukkan titik potong garis dengan sumbu y
Contoh Soal Persamaan Garis Lurus
Misalnya, persamaan garis lurus y = 2x + 3 memiliki gradien 2 dan titik potong sumbu y di titik (0, 3). Artinya, setiap kali nilai x bertambah 1, nilai y akan bertambah 2.
Pentingnya Memahami Persamaan Garis Lurus
Memahami persamaan garis lurus sangat penting dalam pembelajaran matematika kelas 9 karena:
- Menjadi dasar untuk mempelajari konsep matematika lainnya, seperti persamaan kuadrat dan fungsi linear.
- Digunakan dalam berbagai bidang, seperti fisika, ekonomi, dan ilmu komputer.
- Membantu kita memahami hubungan antara dua variabel dan memprediksi nilai salah satu variabel jika nilai variabel lainnya diketahui.
Analisis Soal

Soal-soal matematika di halaman 180 buku teks kelas 9 biasanya mencakup berbagai topik yang telah dipelajari sebelumnya. Untuk memahami dan menyelesaikan soal-soal tersebut, kita perlu mengidentifikasi jenis soal dan langkah-langkah penyelesaian yang tepat.
Butuh bantuan untuk mengerjakan soal matematika kelas 9 halaman 180? Tenang, kamu nggak sendirian! Banyak siswa yang juga merasa kesulitan dengan materi tersebut. Mungkin kamu juga tertarik untuk melihat kunci jawaban fisika kelas 10 kurikulum merdeka yang bisa membantu kamu memahami konsep fisika lebih dalam.
Setelah memahami konsep-konsep fisika, mungkin kamu bisa menemukan cara baru untuk menyelesaikan soal matematika kelas 9 halaman 180. Semangat belajarnya!
Identifikasi Jenis Soal
Untuk menganalisis soal matematika di halaman 180, kita perlu mengetahui jenis soal yang terdapat di dalamnya. Soal-soal di halaman 180 biasanya mencakup beberapa jenis, seperti:
- Soal cerita: Soal yang disajikan dalam bentuk cerita, yang mengharuskan kita untuk memahami cerita dan mengidentifikasi informasi penting untuk menyelesaikan soal.
- Soal hitungan: Soal yang mengharuskan kita untuk melakukan operasi matematika, seperti penjumlahan, pengurangan, perkalian, pembagian, dan lain sebagainya.
- Soal geometri: Soal yang berhubungan dengan bentuk dan ukuran benda, seperti segitiga, persegi, lingkaran, dan lain sebagainya.
- Soal aljabar: Soal yang melibatkan variabel dan persamaan, yang mengharuskan kita untuk menyelesaikan persamaan atau mencari nilai variabel.
Langkah-langkah Penyelesaian Soal
Setelah mengidentifikasi jenis soal, langkah selanjutnya adalah memahami langkah-langkah penyelesaian soal tersebut. Langkah-langkah penyelesaian soal matematika umumnya meliputi:
- Memahami soal: Bacalah soal dengan cermat dan pahami maksud soal.
- Menganalisis soal: Identifikasi informasi penting yang terdapat dalam soal dan tentukan hubungan antar informasi tersebut.
- Menentukan rumus atau konsep yang relevan: Pilih rumus atau konsep yang tepat untuk menyelesaikan soal.
- Menyelesaikan soal: Gunakan rumus atau konsep yang telah dipilih untuk menyelesaikan soal.
- Mengecek kembali jawaban: Pastikan jawaban yang diperoleh benar dan masuk akal.
Contoh Langkah Penyelesaian Soal
Berikut ini adalah contoh langkah penyelesaian soal matematika di halaman 180:
Misalnya, soal cerita yang meminta kita untuk menghitung luas sebuah persegi panjang. Kita perlu memahami cerita dan mengidentifikasi informasi penting, seperti panjang dan lebar persegi panjang. Setelah itu, kita dapat menggunakan rumus luas persegi panjang (L = p x l) untuk menghitung luasnya.
Kemudian, kita perlu mengecek kembali jawaban untuk memastikan kebenarannya.
Konsep Penting
Soal-soal di halaman 180 buku matematika kelas 9 menguji pemahamanmu tentang beberapa konsep penting yang terkait dengan persamaan dan pertidaksamaan linear. Untuk memahaminya dengan lebih baik, mari kita bahas konsep-konsep tersebut secara detail.
Butuh bantuan buat ngerjain soal-soal matematika kelas 9 halaman 180? Tenang, banyak sumber yang bisa kamu akses! Tapi, kalau kamu lagi nyari kunci jawaban buat adik kelas 5, kamu bisa coba cari di kunci jawaban matematika kelas 5 yang banyak tersedia online.
Nah, setelah bantu adikmu, kamu bisa lanjutin ngerjain soal-soal kelas 9 halaman 180 lagi, ya!
Persamaan Linear Satu Variabel
Persamaan linear satu variabel adalah persamaan yang hanya memiliki satu variabel dan pangkat tertinggi dari variabel tersebut adalah 1. Bentuk umum persamaan linear satu variabel adalah ax + b = 0, di mana a dan b adalah konstanta dan x adalah variabel.
- Solusi Persamaan: Solusi persamaan linear satu variabel adalah nilai variabel yang memenuhi persamaan tersebut. Untuk menemukan solusi, kita perlu melakukan operasi aljabar untuk mengisolasi variabel di satu sisi persamaan. Misalnya, untuk menyelesaikan persamaan 2x + 3 = 7, kita dapat mengurangkan 3 dari kedua sisi persamaan untuk mendapatkan 2x = 4, kemudian membagi kedua sisi dengan 2 untuk mendapatkan x = 2.
Jadi, solusi persamaan 2x + 3 = 7 adalah x = 2.
- Grafik Persamaan Linear: Grafik persamaan linear satu variabel adalah garis lurus. Kemiringan garis menunjukkan laju perubahan variabel, sedangkan titik potong sumbu y menunjukkan nilai variabel ketika variabel lainnya bernilai 0. Misalnya, grafik persamaan y = 2x + 1 adalah garis lurus dengan kemiringan 2 dan titik potong sumbu y di (0, 1).
Pertidaksamaan Linear Satu Variabel
Pertidaksamaan linear satu variabel adalah pertidaksamaan yang hanya memiliki satu variabel dan pangkat tertinggi dari variabel tersebut adalah 1. Bentuk umum pertidaksamaan linear satu variabel adalah ax + b > 0, ax + b < 0, ax + b ≥ 0, atau ax + b ≤ 0, di mana a dan b adalah konstanta dan x adalah variabel.
- Solusi Pertidaksamaan: Solusi pertidaksamaan linear satu variabel adalah himpunan nilai variabel yang memenuhi pertidaksamaan tersebut. Untuk menyelesaikan pertidaksamaan, kita dapat menggunakan operasi aljabar yang sama seperti yang digunakan untuk menyelesaikan persamaan, dengan satu pengecualian: jika kita mengalikan atau membagi kedua sisi pertidaksamaan dengan bilangan negatif, tanda pertidaksamaan harus dibalik.
Misalnya, untuk menyelesaikan pertidaksamaan 2x + 3 > 7, kita dapat mengurangkan 3 dari kedua sisi pertidaksamaan untuk mendapatkan 2x > 4, kemudian membagi kedua sisi dengan 2 untuk mendapatkan x > 2. Jadi, solusi pertidaksamaan 2x + 3 > 7 adalah x > 2.
- Grafik Pertidaksamaan Linear: Grafik pertidaksamaan linear satu variabel adalah daerah di bidang koordinat yang memuat semua titik yang memenuhi pertidaksamaan tersebut. Untuk menentukan daerah tersebut, kita dapat menggunakan garis yang mewakili persamaan linear yang terkait dengan pertidaksamaan. Misalnya, grafik pertidaksamaan y > 2x + 1 adalah daerah di atas garis y = 2x + 1.
Sistem Persamaan Linear Dua Variabel
Sistem persamaan linear dua variabel adalah sistem yang terdiri dari dua persamaan linear dengan dua variabel. Bentuk umum sistem persamaan linear dua variabel adalah:
ax + by = cdx + ey = f
di mana a, b, c, d, e, dan f adalah konstanta, dan x dan y adalah variabel.
- Solusi Sistem Persamaan: Solusi sistem persamaan linear dua variabel adalah pasangan nilai (x, y) yang memenuhi kedua persamaan tersebut. Untuk menemukan solusi, kita dapat menggunakan metode eliminasi, substitusi, atau grafik. Metode eliminasi melibatkan menghilangkan satu variabel dengan menambahkan atau mengurangkan kedua persamaan tersebut.
Metode substitusi melibatkan mengisolasi satu variabel dalam satu persamaan dan mensubstitusikannya ke persamaan lainnya. Metode grafik melibatkan menggambar grafik kedua persamaan dan mencari titik potongnya.
Hubungan dengan Materi Lain
Konsep-konsep yang dibahas di atas terkait erat dengan materi lain dalam matematika kelas 9, seperti:
- Aljabar: Persamaan dan pertidaksamaan linear merupakan dasar dari aljabar. Memahami konsep-konsep ini akan membantu Anda dalam menyelesaikan persamaan dan pertidaksamaan yang lebih kompleks di kemudian hari.
- Geometri: Persamaan dan pertidaksamaan linear digunakan untuk menentukan persamaan garis dan daerah dalam geometri.
- Fungsi: Persamaan linear merupakan contoh sederhana dari fungsi. Memahami konsep-konsep ini akan membantu Anda dalam mempelajari fungsi-fungsi yang lebih kompleks di kemudian hari.
Penerapan dalam Kehidupan Sehari-hari
Materi pada halaman 180 buku matematika kelas 9 membahas tentang persamaan linear dua variabel. Persamaan linear dua variabel merupakan konsep matematika yang sangat penting dan memiliki banyak aplikasi dalam kehidupan sehari-hari. Materi ini dapat membantu kita dalam memahami berbagai situasi dan menyelesaikan masalah yang melibatkan hubungan linear antara dua variabel.
Contoh Penerapan dalam Kehidupan Sehari-hari
Persamaan linear dua variabel dapat diterapkan dalam berbagai situasi dalam kehidupan sehari-hari. Berikut adalah beberapa contohnya:
- Perhitungan Biaya: Misalnya, kita ingin menghitung biaya total untuk membeli beberapa barang. Jika harga satu barang adalah Rp10.000 dan kita membeli x barang, maka biaya total (y) dapat dinyatakan dengan persamaan y = 10.000x. Dengan menggunakan persamaan ini, kita dapat menghitung biaya total untuk pembelian dengan jumlah barang yang berbeda.
- Perhitungan Kecepatan: Persamaan linear juga dapat digunakan untuk menghitung kecepatan. Misalnya, jika jarak yang ditempuh adalah 100 km dan waktu tempuh adalah 2 jam, maka kecepatan (v) dapat dinyatakan dengan persamaan v = 100/2 = 50 km/jam. Persamaan ini dapat digunakan untuk menghitung kecepatan dalam berbagai situasi, seperti saat berkendara atau berjalan kaki.
- Perhitungan Suhu: Hubungan antara suhu Celcius (C) dan Fahrenheit (F) dapat dinyatakan dengan persamaan linear F = 9/5C + 32. Persamaan ini dapat digunakan untuk mengkonversi suhu dari Celcius ke Fahrenheit dan sebaliknya.
Manfaat Mempelajari Materi Persamaan Linear Dua Variabel, Kunci jawaban matematika kelas 9 halaman 180
Mempelajari materi persamaan linear dua variabel memiliki beberapa manfaat dalam kehidupan nyata, yaitu:
- Meningkatkan Kemampuan Pemecahan Masalah: Mempelajari persamaan linear dua variabel membantu kita dalam mengembangkan kemampuan untuk memecahkan masalah yang melibatkan hubungan linear antara dua variabel. Kita dapat menggunakan persamaan linear untuk menganalisis situasi, mencari solusi, dan membuat prediksi.
- Meningkatkan Kemampuan Berpikir Logis: Materi ini melatih kemampuan berpikir logis dan analitis. Dengan memahami konsep persamaan linear dua variabel, kita dapat menalar secara sistematis dan menemukan hubungan yang tersembunyi dalam berbagai situasi.
- Mempersiapkan Diri untuk Jenjang Pendidikan Selanjutnya: Materi persamaan linear dua variabel merupakan dasar penting untuk mempelajari konsep matematika yang lebih lanjut, seperti aljabar, kalkulus, dan statistika. Dengan memahami konsep ini, kita akan lebih siap untuk menghadapi tantangan di jenjang pendidikan selanjutnya.
Cara Materi Ini Membantu Menyelesaikan Masalah Sehari-hari
Persamaan linear dua variabel dapat membantu kita dalam menyelesaikan berbagai masalah sehari-hari, seperti:
- Perencanaan Keuangan: Persamaan linear dapat digunakan untuk membuat anggaran dan merencanakan pengeluaran. Misalnya, kita dapat membuat persamaan linear untuk menghitung biaya hidup bulanan berdasarkan pengeluaran untuk makanan, transportasi, dan kebutuhan lainnya.
- Perhitungan Waktu: Persamaan linear dapat digunakan untuk menghitung waktu yang dibutuhkan untuk menyelesaikan suatu pekerjaan atau mencapai tujuan tertentu. Misalnya, kita dapat membuat persamaan linear untuk menghitung waktu yang dibutuhkan untuk menyelesaikan proyek berdasarkan kecepatan kerja dan jumlah pekerjaan.
- Analisis Data: Persamaan linear dapat digunakan untuk menganalisis data dan menemukan pola hubungan antara dua variabel. Misalnya, kita dapat menggunakan persamaan linear untuk menganalisis data tentang pertumbuhan penduduk atau perubahan harga suatu barang.
Tips dan Trik
Menjelajahi dunia matematika bisa jadi menyenangkan dan menantang. Untuk menaklukkan soal-soal di halaman 180 dan soal-soal serupa, kamu bisa menggunakan beberapa tips dan trik. Strategi yang tepat dapat membantumu menyelesaikan soal matematika dengan cepat dan tepat. Mari kita bahas beberapa strategi dan contoh soal yang bisa kamu coba!
Memahami Konsep Dasar
Langkah pertama yang penting adalah memahami konsep dasar yang mendasari soal-soal tersebut. Pahami definisi, rumus, dan teorema yang terkait dengan materi tersebut. Misalnya, jika kamu menghadapi soal tentang persamaan linear, pastikan kamu memahami konsep persamaan linear, cara menyelesaikannya, dan bagaimana menentukan nilai variabel.
Bingung dengan soal-soal matematika kelas 9 halaman 180? Tenang, kamu nggak sendirian! Banyak siswa yang juga mengalami kesulitan memahami konsep dan menyelesaikan soal-soal di halaman tersebut. Kamu bisa menemukan panduan dan jawaban di berbagai sumber, termasuk situs web yang menyediakan kunci jawaban.
Misalnya, kamu bisa menemukan kunci jawaban untuk PKN kelas 9 halaman 66 di situs ini , yang bisa membantu kamu memahami materi PKN lebih dalam. Dengan memahami materi PKN, kamu bisa lebih mudah untuk fokus kembali ke materi matematika kelas 9 halaman 180 dan menyelesaikan soal-soal dengan lebih percaya diri.
- Bacalah materi pelajaran dengan seksama. Pastikan kamu memahami konsep dan rumus yang dijelaskan.
- Buat catatan ringkas dari materi pelajaran yang penting. Catatan ini akan membantumu mengingat konsep-konsep penting dengan mudah.
- Berlatihlah mengerjakan soal-soal latihan yang berkaitan dengan konsep yang sedang dipelajari. Semakin banyak latihan, semakin kuat pemahamanmu.
Strategi Penyelesaian Soal
Setelah memahami konsep dasar, kamu perlu menerapkan strategi yang tepat untuk menyelesaikan soal matematika dengan cepat dan tepat. Berikut beberapa strategi yang bisa kamu coba:
- Baca soal dengan cermat:Pastikan kamu memahami apa yang diminta dalam soal. Identifikasi informasi yang diberikan dan apa yang ingin kamu cari.
- Identifikasi jenis soal:Tentukan jenis soal yang sedang kamu hadapi. Apakah itu soal persamaan, pertidaksamaan, geometri, atau lainnya? Ini akan membantumu memilih strategi yang tepat.
- Buat sketsa atau diagram:Jika memungkinkan, buat sketsa atau diagram untuk membantu memvisualisasikan soal. Ini bisa memudahkanmu untuk memahami hubungan antar variabel.
- Tuliskan rumus yang relevan:Sebelum memulai perhitungan, tuliskan rumus yang relevan dengan soal tersebut. Ini akan membantumu menghindari kesalahan dalam memilih rumus yang tepat.
- Kerjakan langkah demi langkah:Hindari melakukan terlalu banyak langkah sekaligus. Kerjakan soal secara bertahap dan teliti.
- Periksa kembali jawaban:Setelah menyelesaikan soal, pastikan kamu memeriksa kembali jawabanmu. Pastikan jawabanmu masuk akal dan sesuai dengan konteks soal.
Contoh Soal Latihan
Untuk mengasah pemahaman dan menguji kemampuanmu, cobalah mengerjakan contoh soal latihan berikut. Contoh ini dapat membantumu memahami penerapan konsep dan strategi yang telah dibahas sebelumnya.
- Soal 1:Tentukan nilai x yang memenuhi persamaan 2x + 5 = 11.
- Soal 2:Hitunglah luas segitiga dengan alas 10 cm dan tinggi 8 cm.
- Soal 3:Sebuah mobil melaju dengan kecepatan 60 km/jam. Berapa jarak yang ditempuh mobil tersebut dalam waktu 2 jam?
Cobalah untuk menyelesaikan soal-soal latihan tersebut. Jika kamu mengalami kesulitan, jangan ragu untuk meminta bantuan guru atau teman sekelasmu. Ingatlah, latihan adalah kunci untuk menguasai matematika.
Ulasan Penutup
Dengan memahami konsep-konsep penting dan menerapkan tips dan trik yang telah dibahas, kamu akan lebih mudah dalam menyelesaikan soal-soal matematika kelas 9, khususnya yang terdapat pada halaman 180. Jangan ragu untuk berlatih dan bertanya jika ada kesulitan. Ingat, matematika bukanlah monster menakutkan, tetapi sebuah ilmu yang menarik dan bermanfaat untuk kehidupan!
Area Tanya Jawab
Apakah materi di halaman 180 sulit?
Tingkat kesulitan materi di halaman 180 tergantung pada pemahaman dasarmu terhadap konsep-konsep sebelumnya. Jika kamu merasa kesulitan, jangan ragu untuk bertanya kepada guru atau mencari bantuan tambahan.
Apakah ada latihan soal tambahan selain yang ada di buku?
Ya, kamu bisa menemukan latihan soal tambahan di buku-buku latihan, website pendidikan, atau aplikasi belajar online.
Bagaimana cara memahami materi matematika dengan lebih baik?
Cobalah untuk menghubungkan materi dengan contoh-contoh nyata dalam kehidupan sehari-hari. Jangan takut untuk bertanya jika ada yang tidak dipahami. Dan yang terpenting, rajinlah berlatih!