Kunci jawaban matematika kelas 8 halaman 127 – Pernah merasa kesulitan memahami materi matematika di kelas 8, khususnya di halaman 127? Tenang, kamu tidak sendirian! Halaman ini biasanya membahas materi yang cukup menantang, namun dengan pemahaman yang tepat, semua akan terasa lebih mudah. Artikel ini akan menjadi panduan lengkapmu untuk menguasai materi di halaman 127, mulai dari penjelasan konsep, contoh soal, hingga penerapannya dalam kehidupan sehari-hari.
Mari kita telusuri lebih dalam tentang materi yang dibahas di halaman 127, seperti jenis soal, konsep-konsep matematika yang terlibat, dan langkah-langkah penyelesaiannya. Artikel ini juga akan memberikan contoh soal tambahan dan membahas kesalahan umum yang sering terjadi dalam menyelesaikan soal-soal di halaman 127. Siap untuk menaklukkan tantangan matematika di halaman ini?
Konteks Soal: Kunci Jawaban Matematika Kelas 8 Halaman 127

Halaman 127 buku pelajaran matematika kelas 8 kemungkinan besar membahas tentang persamaan linear satu variabel. Materi ini merupakan dasar dalam aljabar, yang membantu kita memahami dan menyelesaikan berbagai masalah yang melibatkan variabel tunggal. Soal-soal yang terdapat di halaman tersebut biasanya bertujuan untuk menguji pemahaman kita tentang konsep persamaan linear, cara menyelesaikannya, dan penerapannya dalam situasi nyata.
Persamaan Linear Satu Variabel
Persamaan linear satu variabel adalah persamaan yang hanya memiliki satu variabel, dan variabel tersebut berpangkat satu. Bentuk umum persamaan linear satu variabel adalah:
ax + b = c
di mana:
- x adalah variabel
- a, b, dan c adalah konstanta
Tujuan utama dalam menyelesaikan persamaan linear satu variabel adalah mencari nilai x yang memenuhi persamaan tersebut. Untuk menemukan nilai x, kita dapat menggunakan berbagai metode, seperti:
- Metode eliminasi
- Metode substitusi
- Metode gabungan
Contoh Soal dan Penyelesaian
Misalkan terdapat soal pada halaman 127 yang berbunyi: “Tentukan nilai x yang memenuhi persamaan 2x + 5 = 11.” Untuk menyelesaikan soal ini, kita dapat menggunakan metode eliminasi.
- Kurangi 5 dari kedua ruas persamaan:
- Sederhanakan persamaan:
- Bagi kedua ruas persamaan dengan 2:
- Sederhanakan persamaan:
- Kurangi kedua ruas persamaan dengan 5:
- 2x + 5 – 5 = 11 – 5
- 2x = 6
- Bagi kedua ruas persamaan dengan 2:
- 2x / 2 = 6 / 2
- x = 3
- Salah dalam melakukan operasi matematika, seperti penjumlahan, pengurangan, perkalian, dan pembagian.
- Salah dalam mengidentifikasi koefisien dan konstanta dalam persamaan.
- Tidak memperhatikan tanda positif dan negatif dalam persamaan.
- Tambahkan 7 ke kedua ruas persamaan:
- 3x – 7 + 7 = 8 + 7
- 3x = 15
- Bagi kedua ruas persamaan dengan 3:
- 3x / 3 = 15 / 3
- x = 5
- Perencanaan Keuangan: Konsep persamaan linear dapat digunakan untuk menghitung pengeluaran bulanan, merencanakan anggaran, dan mengelola keuangan pribadi. Misalnya, dengan persamaan linear, kita dapat menghitung total biaya yang dikeluarkan untuk kebutuhan pokok seperti makanan, transportasi, dan tagihan bulanan.
- Pembelian Barang: Ketika membeli barang, kita dapat menggunakan konsep persentase untuk menghitung diskon, pajak, dan harga akhir. Misalnya, jika sebuah baju di diskon 20%, kita dapat menggunakan persentase untuk menghitung harga diskon dan harga akhir yang harus dibayarkan.
- Pengukuran dan Konstruksi: Konsep geometri, seperti luas dan volume, sangat penting dalam bidang konstruksi dan desain. Misalnya, untuk menghitung luas ruangan atau volume sebuah wadah, kita dapat menggunakan rumus geometri yang dipelajari di halaman 127.
- Tepung: 2 cangkir –> 1,5 cangkir (berkurang 0,5 cangkir)
- Gula: 1 cangkir –> 1 cangkir – (0,5 cangkir/2) = 0,75 cangkir
- Mentega: 1/2 cangkir –> (1/2 cangkir)
-(0,5 cangkir/4) = 0,375 cangkir - Contohnya, persamaan 2x + 3y = 6 merupakan persamaan linear dua variabel dengan variabel x dan y.
- Sistem persamaan linear dua variabel adalah kumpulan dari dua atau lebih persamaan linear yang memiliki variabel yang sama.
- Pemahaman tentang persamaan linear dua variabel sangat penting untuk menyelesaikan sistem persamaan linear dua variabel dengan berbagai metode, seperti metode substitusi, eliminasi, dan grafik.
- Sistem persamaan linear tiga variabel: Persamaan linear dua variabel menjadi dasar untuk memahami konsep sistem persamaan linear tiga variabel, yang melibatkan tiga variabel dan tiga persamaan linear.
- Fungsi linear: Persamaan linear dua variabel merupakan bentuk dasar dari fungsi linear, yang dapat divisualisasikan sebagai garis lurus pada bidang koordinat.
- Persamaan kuadrat: Persamaan linear dua variabel merupakan bagian penting dalam menyelesaikan persamaan kuadrat, khususnya dalam mencari titik potong grafik persamaan kuadrat dengan sumbu x dan sumbu y.
x + 5 – 5 = 11 – 5
– x = 6
– x / 2 = 6 / 2
Sedang cari kunci jawaban matematika kelas 8 halaman 127? Tenang, banyak sumber yang bisa kamu temukan di internet. Tapi, kalau kamu lagi cari kunci jawaban untuk materi lain, seperti contohnya kunci jawaban tema 6 kelas 6 halaman 50, kamu bisa cek di situs ini. Situs ini menyediakan berbagai macam kunci jawaban, termasuk untuk pelajaran matematika kelas 8 halaman 127, lho!
x = 3
Jadi, nilai x yang memenuhi persamaan 2x + 5 = 11 adalah x = 3.
Pembahasan Soal
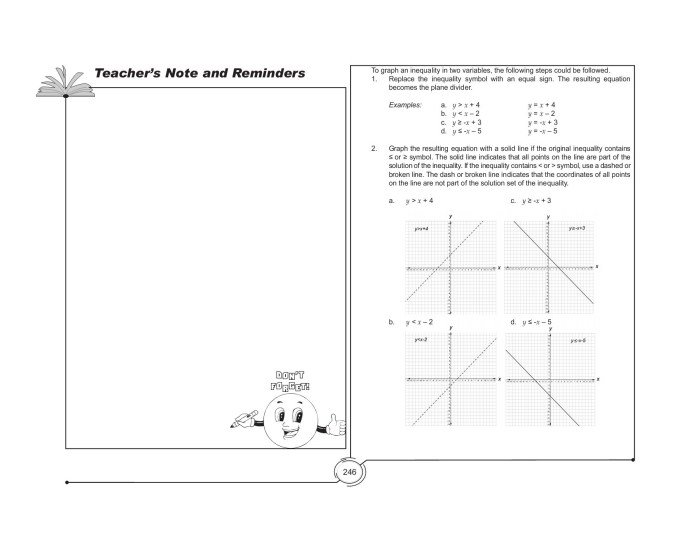
Materi di halaman 127 buku matematika kelas 8 membahas tentang persamaan linear satu variabel. Persamaan linear satu variabel adalah persamaan yang hanya memiliki satu variabel dengan pangkat tertinggi 1. Untuk menyelesaikan persamaan linear satu variabel, kita perlu menemukan nilai variabel yang membuat persamaan tersebut benar.
Rumus-rumus Matematika
Berikut adalah tabel yang merangkum rumus-rumus matematika yang digunakan dalam soal-soal di halaman 127:
| Rumus | Keterangan |
|---|---|
| ax + b = c | Persamaan linear satu variabel, dengan a, b, dan c adalah konstanta. |
| x = (c – b) / a | Rumus untuk mencari nilai x dalam persamaan linear satu variabel. |
Contoh Soal dan Penyelesaian
Berikut adalah contoh soal dan penyelesaiannya:
2x + 5 = 11
Langkah-langkah penyelesaian:
Jadi, nilai x yang memenuhi persamaan 2x + 5 = 11 adalah x = 3.
Kesalahan Umum
Kesalahan umum yang sering terjadi dalam menyelesaikan soal-soal di halaman 127 adalah:
Contoh Soal Tambahan
Berikut adalah contoh soal tambahan yang sejenis dengan soal di halaman 127:
3x – 7 = 8
Butuh bantuan buat ngerjain soal-soal matematika kelas 8 halaman 127? Tenang, banyak sumber yang bisa kamu akses. Tapi, sebelum itu, pernah ngerjain soal-soal matematika kelas 7 halaman 84? Kalau belum, kamu bisa cek kunci jawaban matematika kelas 7 halaman 84 di website ini. Nah, balik lagi ke soal kelas 8, pastikan kamu pahami konsepnya, ya! Jangan cuma ngandalin kunci jawaban.
Pahami konsepnya, latihan soal, dan kamu pasti bisa ngerjain soal-soal matematika kelas 8 halaman 127 dengan mudah!
Penyelesaian:
Jadi, nilai x yang memenuhi persamaan 3x – 7 = 8 adalah x = 5.
Bingung sama soal matematika kelas 8 halaman 127? Tenang, kamu nggak sendirian! Banyak banget yang juga nyari kunci jawabannya. Nah, kalau kamu lagi nyari kunci jawaban kelas 6 tema 4 halaman 119, bisa cek di kunci jawaban kelas 6 tema 4 halaman 119. Setelah itu, kamu bisa fokus lagi ke soal matematika kelas 8 halaman 127. Semangat belajarnya!
Penerapan Konsep

Konsep matematika yang dipelajari di halaman 127 memiliki aplikasi luas dalam kehidupan sehari-hari, membantu kita memahami dan memecahkan berbagai masalah. Konsep-konsep ini tidak hanya terbatas pada dunia akademis, tetapi juga membantu kita dalam membuat keputusan yang rasional dan efektif dalam berbagai situasi.
Penerapan Konsep dalam Kehidupan Sehari-hari
Konsep matematika yang dipelajari di halaman 127 dapat diterapkan dalam berbagai aspek kehidupan sehari-hari, seperti:
Contoh Skenario Nyata
Bayangkan Anda ingin merencanakan liburan ke suatu tempat. Anda memiliki anggaran terbatas dan ingin mencari hotel yang sesuai dengan budget. Anda dapat menggunakan konsep persamaan linear untuk menghitung biaya total liburan, termasuk biaya transportasi, akomodasi, dan makanan. Dengan persamaan linear, Anda dapat menentukan batas maksimal biaya yang dapat Anda keluarkan untuk akomodasi dan menyesuaikan pilihan hotel sesuai dengan budget yang tersedia.
Masalah dan Solusi
Anda ingin membuat kue ulang tahun untuk teman Anda. Resep kue tersebut membutuhkan 2 cangkir tepung, 1 cangkir gula, dan 1/2 cangkir mentega. Anda hanya memiliki 1,5 cangkir tepung. Berapa banyak gula dan mentega yang harus Anda gunakan agar proporsi bahan tetap sama?Solusi:Anda dapat menggunakan konsep perbandingan untuk menyelesaikan masalah ini. Karena tepung yang tersedia hanya 1,5 cangkir, maka proporsi bahan harus disesuaikan.
Jadi, Anda perlu menggunakan 0,75 cangkir gula dan 0,375 cangkir mentega agar proporsi bahan tetap sama.
Ilustrasi Penerapan Konsep
Bayangkan sebuah toko pakaian yang memberikan diskon 20% untuk semua barang. Anda dapat menggunakan konsep persentase untuk menghitung harga diskon dan harga akhir yang harus dibayarkan. Misalnya, jika harga awal sebuah baju adalah Rp100.000, maka harga diskonnya adalah 20% x Rp100.000 = Rp20.000. Harga akhir yang harus dibayarkan adalah Rp100.000 – Rp20.000 = Rp80.000. Ilustrasi ini menunjukkan bagaimana konsep persentase dapat diterapkan dalam kehidupan sehari-hari, khususnya dalam kegiatan berbelanja.
Kaitan dengan Materi Lain

Materi matematika di halaman 127 membahas tentang persamaan linear dua variabel. Materi ini memiliki keterkaitan erat dengan materi lain yang telah dipelajari di kelas 8, seperti sistem persamaan linear dua variabel, fungsi linear, dan bahkan konsep persamaan dalam aljabar.
Hubungan dengan Sistem Persamaan Linear Dua Variabel
Materi persamaan linear dua variabel merupakan fondasi untuk mempelajari sistem persamaan linear dua variabel. Persamaan linear dua variabel sendiri merupakan persamaan yang melibatkan dua variabel dengan pangkat tertinggi 1.
Contoh Soal Gabungan
Berikut contoh soal yang menggabungkan konsep persamaan linear dua variabel dengan sistem persamaan linear dua variabel:
“Sebuah toko menjual dua jenis kue, kue A dan kue B. Harga satu kue A adalah Rp 10.000 dan harga satu kue B adalah Rp 15.000. Pada hari Sabtu, toko tersebut menjual 20 kue A dan 15 kue B, dan mendapatkan total pendapatan Rp 375.000. Tentukan banyak kue A dan kue B yang terjual pada hari Sabtu.”
Dalam soal ini, kita dapat membentuk sistem persamaan linear dua variabel untuk menyelesaikan masalah tersebut.
Kutipan Buku Pelajaran
“Persamaan linear dua variabel merupakan persamaan yang dapat dinyatakan dalam bentuk ax + by = c, dengan a, b, dan c adalah konstanta dan a dan b tidak sama dengan nol. Persamaan ini sangat penting dalam menyelesaikan masalah-masalah yang melibatkan dua variabel, seperti dalam sistem persamaan linear dua variabel, yang terdiri dari dua atau lebih persamaan linear yang memiliki variabel yang sama.”
Manfaat dalam Mempelajari Materi Selanjutnya, Kunci jawaban matematika kelas 8 halaman 127
Pemahaman yang kuat tentang persamaan linear dua variabel akan membantu dalam mempelajari materi matematika selanjutnya, seperti:
Dengan memahami konsep dan latihan yang cukup, kamu akan mampu menguasai materi di halaman 127 dengan percaya diri. Ingat, matematika tidak hanya tentang rumus, tetapi juga tentang pemahaman dan penerapannya dalam kehidupan nyata. Jadi, jangan ragu untuk terus belajar dan berlatih, dan jangan lupa untuk selalu bertanya jika ada hal yang belum jelas.
Informasi Penting & FAQ
Apakah halaman 127 membahas tentang persamaan linear?
Kemungkinan besar ya, karena persamaan linear merupakan materi umum di kelas 8. Tapi untuk memastikan, kamu perlu melihat buku pelajaranmu.
Apakah ada contoh soal di halaman 127 yang menggunakan rumus Pythagoras?
Mungkin saja, karena rumus Pythagoras juga merupakan materi penting di kelas 8. Periksa buku pelajaranmu untuk memastikan.