Kunci jawaban matematika kelas 9 halaman 87 88 – Pernah merasa kesulitan memahami materi matematika di kelas 9, khususnya pada halaman 87-88? Tenang, kamu tidak sendirian! Kunci Jawaban Matematika Kelas 9 Halaman 87-88 ini hadir untuk membantumu menguasai konsep dan strategi dalam menyelesaikan soal-soal yang ada. Dengan panduan yang jelas dan terstruktur, kamu akan menemukan jawaban atas pertanyaan-pertanyaan yang selama ini membingungkan.
Artikel ini akan membahas secara detail materi yang dipelajari pada halaman 87-88, menganalisis jenis soal yang dijumpai, dan memberikan strategi jitu untuk menyelesaikannya. Selain itu, kamu juga akan menemukan penerapan konsep matematika dalam kehidupan sehari-hari, sehingga pemahamanmu semakin kuat dan tertanam.
Memahami Soal Matematika Kelas 9 Halaman 87-88
Halaman 87-88 buku Matematika Kelas 9 membahas tentang persamaan kuadrat. Persamaan kuadrat adalah persamaan yang memiliki pangkat tertinggi dari variabelnya adalah dua. Dalam halaman ini, kamu akan belajar bagaimana menyelesaikan persamaan kuadrat dengan berbagai metode, seperti memfaktorkan, melengkapi kuadrat, dan menggunakan rumus kuadrat.
Pengertian Persamaan Kuadrat
Persamaan kuadrat adalah persamaan yang memiliki bentuk umum ax² + bx + c = 0, di mana a, b, dan c adalah konstanta dan a ≠ 0. Koefisien a, b, dan c menentukan sifat persamaan kuadrat, seperti bentuk grafiknya, jumlah akar-akarnya, dan diskriminannya.
Metode Penyelesaian Persamaan Kuadrat
Ada beberapa metode yang dapat digunakan untuk menyelesaikan persamaan kuadrat, yaitu:
- Memfaktorkan: Metode ini melibatkan pemfaktoran persamaan kuadrat menjadi dua faktor linear. Setelah difaktorkan, akar-akar persamaan dapat ditemukan dengan menetapkan setiap faktor sama dengan nol.
- Melengkapi Kuadrat: Metode ini melibatkan manipulasi persamaan kuadrat sehingga menjadi bentuk (x + h)² = k, di mana h dan k adalah konstanta. Setelah persamaan dalam bentuk ini, akar-akarnya dapat ditemukan dengan mengambil akar kuadrat dari kedua ruas persamaan.
- Rumus Kuadrat: Rumus kuadrat adalah rumus yang digunakan untuk menemukan akar-akar persamaan kuadrat. Rumus ini dapat digunakan untuk menyelesaikan persamaan kuadrat apa pun, terlepas dari apakah persamaan tersebut dapat difaktorkan atau tidak.
Contoh Soal dan Penyelesaian
Contoh soal dari halaman 87-88 adalah:
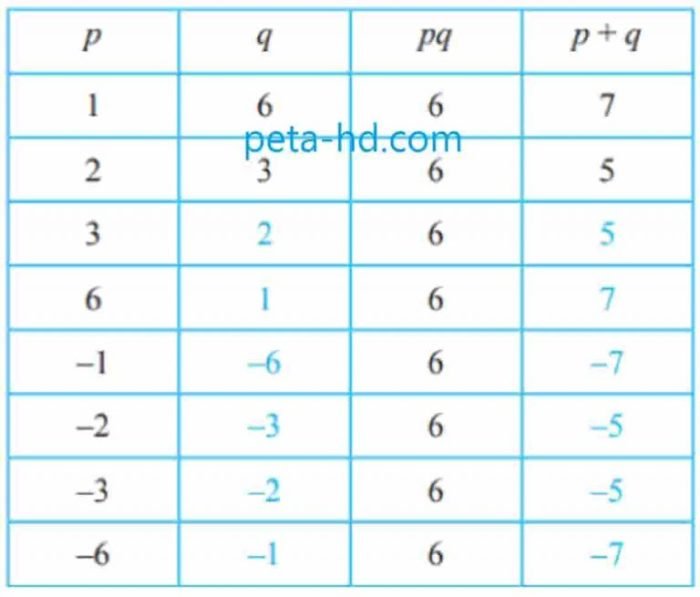
Tentukan akar-akar persamaan kuadrat x² + 5x + 6 = 0.
Untuk menyelesaikan persamaan ini, kita dapat menggunakan metode memfaktorkan. Persamaan ini dapat difaktorkan menjadi (x + 2)(x + 3) = 0. Dengan menetapkan setiap faktor sama dengan nol, kita memperoleh x + 2 = 0 atau x + 3 = 0. Oleh karena itu, akar-akar persamaan kuadrat adalah x = -2 dan x = -3.
Rumus-rumus Penting
| Rumus | Keterangan |
|---|---|
| ax² + bx + c = 0 | Bentuk umum persamaan kuadrat |
x = (-b ± √(b²
|
Rumus kuadrat |
| D = b² – 4ac | Diskriminan persamaan kuadrat |
Pertanyaan yang Mungkin Muncul
Beberapa pertanyaan yang mungkin muncul dari soal-soal halaman 87-88 adalah:
- Bagaimana cara menentukan jenis akar-akar persamaan kuadrat?
- Bagaimana cara menentukan nilai diskriminan persamaan kuadrat?
- Bagaimana cara menyelesaikan persamaan kuadrat dengan menggunakan rumus kuadrat?
- Bagaimana cara menggambar grafik persamaan kuadrat?
Menganalisis Jenis Soal

Soal-soal matematika di halaman 87-88 buku teks kelas 9 memiliki beragam jenis yang menguji pemahamanmu terhadap konsep-konsep yang telah dipelajari. Menganalisis jenis-jenis soal ini akan membantumu memahami karakteristiknya, strategi penyelesaian, dan mempersiapkan diri untuk menghadapi soal-soal serupa di masa mendatang.
Soal Persamaan Linear Satu Variabel
Soal persamaan linear satu variabel biasanya melibatkan persamaan yang hanya memiliki satu variabel (biasanya ‘x’ atau ‘y’) dan pangkat tertinggi variabelnya adalah 1. Persamaan ini dapat ditulis dalam bentuk ax + b = c, di mana a, b, dan c adalah konstanta. Untuk menyelesaikan soal ini, kamu perlu menemukan nilai variabel yang memenuhi persamaan tersebut.
Butuh bantuan untuk mengerjakan soal matematika kelas 9 halaman 87-88? Tenang, banyak sumber belajar yang bisa kamu gunakan. Ingat, belajar itu penting, dan kunci jawaban hanyalah panduan untuk membantu kamu memahami konsep. Nah, kalau kamu lagi nyari kunci jawaban bahasa Indonesia kelas 10 halaman 17 kurikulum merdeka, coba cek kunci jawaban bahasa indonesia kelas 10 halaman 17 kurikulum merdeka.
Semoga bisa membantumu belajar lebih efektif. Dan ingat, belajar itu bukan tentang menghafal, tapi tentang memahami dan menerapkan konsep. Selamat belajar!
- Karakteristik: Soal ini biasanya berupa persamaan yang melibatkan satu variabel, dengan pangkat tertinggi variabelnya adalah
1. Contoh: 2x + 5 = 11 - Cara Penyelesaian: Untuk menyelesaikan soal ini, kamu dapat menggunakan operasi aljabar seperti penjumlahan, pengurangan, perkalian, dan pembagian untuk mengisolasi variabel pada satu sisi persamaan. Contoh:
2x + 5 = 11
2x = 11 – 5
2x = 6
x = 6/2
x = 3Bingung sama soal matematika kelas 9 halaman 87 dan 88? Tenang, kamu nggak sendirian! Banyak yang ngalamin hal yang sama. Nah, buat kamu yang lagi nyari kunci jawabannya, bisa coba cek website kunci jawaban kelas 10 yang mungkin punya informasi tambahan yang bisa kamu manfaatin. Tapi inget, kunci jawaban itu cuma sebagai panduan, bukan untuk ditiru begitu aja ya.
Pahami konsepnya dulu baru liat kunci jawabannya. Semangat belajarnya!
Soal Pertidaksamaan Linear Satu Variabel
Soal pertidaksamaan linear satu variabel mirip dengan persamaan linear satu variabel, tetapi melibatkan tanda pertidaksamaan ( <, >, ≤, ≥) di antara dua ekspresi aljabar. Pertidaksamaan ini menyatakan hubungan antara dua ekspresi, bukan persamaan yang tepat.
- Karakteristik: Soal ini melibatkan tanda pertidaksamaan ( <, >, ≤, ≥) dan satu variabel dengan pangkat tertinggi
1. Contoh: 3x – 4 < 10 - Cara Penyelesaian: Penyelesaian pertidaksamaan mirip dengan penyelesaian persamaan, tetapi ada beberapa hal yang perlu diperhatikan:
- Jika dikalikan atau dibagi dengan bilangan negatif, tanda pertidaksamaan harus dibalik.
- Solusi pertidaksamaan biasanya berupa rentang nilai, bukan hanya satu nilai tunggal.
Contoh:
3x – 4 < 10 3x < 10 + 4 3x < 14 x < 14/3
Solusi: x < 14/3
Soal Sistem Persamaan Linear Dua Variabel
Soal sistem persamaan linear dua variabel melibatkan dua persamaan linear yang memiliki dua variabel (biasanya ‘x’ dan ‘y’). Untuk menyelesaikan sistem persamaan ini, kamu perlu mencari nilai ‘x’ dan ‘y’ yang memenuhi kedua persamaan tersebut.
- Karakteristik: Soal ini melibatkan dua persamaan linear dengan dua variabel. Contoh:
2x + 3y = 10
x – y = 1 - Cara Penyelesaian: Ada beberapa metode yang dapat digunakan untuk menyelesaikan sistem persamaan linear dua variabel, antara lain:
- Metode Substitusi: Memecahkan salah satu persamaan untuk satu variabel dan mensubstitusikannya ke persamaan lainnya.
- Metode Eliminasi: Mengalikan kedua persamaan dengan konstanta yang sesuai sehingga koefisien salah satu variabel menjadi sama, lalu mengurangi kedua persamaan untuk menghilangkan variabel tersebut.
- Metode Grafik: Menggambar grafik kedua persamaan pada bidang kartesius dan menentukan titik potong kedua garis tersebut.
Soal Pertidaksamaan Linear Dua Variabel
Soal pertidaksamaan linear dua variabel mirip dengan sistem persamaan linear dua variabel, tetapi melibatkan tanda pertidaksamaan ( <, >, ≤, ≥) di antara dua ekspresi aljabar. Pertidaksamaan ini menyatakan hubungan antara dua ekspresi, bukan persamaan yang tepat.
- Karakteristik: Soal ini melibatkan tanda pertidaksamaan ( <, >, ≤, ≥) dan dua variabel dengan pangkat tertinggi
1. Contoh: 2x + y ≤ 5 - Cara Penyelesaian: Penyelesaian pertidaksamaan dua variabel mirip dengan penyelesaian pertidaksamaan satu variabel, tetapi solusinya berupa daerah pada bidang kartesius, bukan hanya satu nilai tunggal.
- Ubah tanda pertidaksamaan menjadi tanda persamaan dan gambar garisnya pada bidang kartesius.
- Pilih titik uji di salah satu sisi garis dan substitusikan titik tersebut ke dalam pertidaksamaan awal. Jika titik tersebut memenuhi pertidaksamaan, maka daerah yang berisi titik tersebut merupakan solusi pertidaksamaan.
Perbedaan dan Persamaan Jenis Soal
| Jenis Soal | Karakteristik | Cara Penyelesaian | Persamaan | Perbedaan |
|---|---|---|---|---|
| Persamaan Linear Satu Variabel | Satu variabel, pangkat tertinggi 1, tanda ‘=’ | Operasi aljabar untuk mengisolasi variabel | Memiliki satu variabel | Hanya memiliki satu solusi |
| Pertidaksamaan Linear Satu Variabel | Satu variabel, pangkat tertinggi 1, tanda ‘<', '>‘, ‘≤’, ‘≥’ | Operasi aljabar dengan memperhatikan tanda pertidaksamaan | Memiliki satu variabel | Memiliki rentang solusi |
| Sistem Persamaan Linear Dua Variabel | Dua persamaan linear dengan dua variabel | Metode substitusi, eliminasi, atau grafik | Memiliki dua variabel | Memiliki dua solusi (x, y) |
| Pertidaksamaan Linear Dua Variabel | Dua variabel, pangkat tertinggi 1, tanda ‘<', '>‘, ‘≤’, ‘≥’ | Menggambar garis dan memilih titik uji | Memiliki dua variabel | Memiliki daerah solusi pada bidang kartesius |
Strategi Menyelesaikan Soal

Matematika adalah pelajaran yang membutuhkan pemahaman konsep dan latihan yang konsisten. Untuk menyelesaikan soal matematika dengan efektif, diperlukan strategi yang tepat. Berikut beberapa strategi umum yang dapat diterapkan untuk menyelesaikan soal-soal matematika, khususnya yang ada di halaman 87-88 buku pelajaran kelas 9.
Memahami Soal
Langkah pertama yang penting adalah memahami soal dengan baik. Pastikan kamu mengerti apa yang diminta dan apa yang diketahui dalam soal. Bacalah soal dengan cermat dan identifikasi kata kunci yang menunjukkan operasi matematika yang harus dilakukan. Misalnya, kata “jumlah” mengindikasikan penjumlahan, “selisih” mengindikasikan pengurangan, “kali” mengindikasikan perkalian, dan “bagi” mengindikasikan pembagian.
Membuat Diagram atau Gambar
Membuat diagram atau gambar dapat membantu memvisualisasikan soal dan mempermudah pemahaman. Misalnya, jika soal membahas tentang bangun ruang, membuat gambar bangun ruang tersebut dapat membantu kamu melihat hubungan antar sisi dan sudut. Selain itu, diagram juga dapat membantu dalam mengidentifikasi informasi yang relevan dan menyusun strategi penyelesaian.
Butuh bantuan untuk menyelesaikan soal matematika kelas 9 halaman 87 dan 88? Tenang, kamu nggak sendirian! Banyak siswa yang merasa kesulitan dengan materi tersebut. Nah, kalau kamu lagi nyari kunci jawaban untuk game “Wow” level 435, bisa cek di kunci jawaban wow level 435. Semoga artikel ini bisa membantu kamu untuk menyelesaikan soal-soal matematika kelas 9 halaman 87 dan 88 dengan lebih mudah!
Mencari Pola dan Hubungan, Kunci jawaban matematika kelas 9 halaman 87 88
Dalam beberapa soal matematika, terdapat pola atau hubungan yang dapat membantu dalam menyelesaikan soal. Perhatikan dengan seksama data yang diberikan dan carilah pola atau hubungan yang mungkin ada. Misalnya, jika soal membahas tentang barisan aritmatika, carilah selisih tetap antar suku. Pola atau hubungan ini dapat membantu dalam menentukan nilai suku berikutnya atau rumus umum barisan.
Mencoba Strategi yang Berbeda
Jika kamu kesulitan menyelesaikan soal dengan satu strategi, cobalah strategi yang berbeda. Ada banyak cara untuk menyelesaikan suatu soal matematika, dan menemukan cara yang paling efektif untukmu mungkin membutuhkan percobaan. Misalnya, jika kamu kesulitan menyelesaikan soal persamaan linear, cobalah menggunakan metode substitusi atau eliminasi.
Memeriksa Kembali Jawaban
Setelah mendapatkan jawaban, periksa kembali jawabanmu untuk memastikan keakuratannya. Gunakan metode yang berbeda untuk memverifikasi jawabanmu, atau cobalah mengganti jawabanmu ke dalam soal asli untuk melihat apakah hasilnya sesuai.
Tips dan Trik
- Latihlah secara rutin untuk meningkatkan kemampuan menyelesaikan soal matematika.
- Jangan takut untuk bertanya kepada guru atau teman jika kamu mengalami kesulitan.
- Manfaatkan sumber belajar yang tersedia, seperti buku, internet, dan aplikasi edukasi.
- Tetap tenang dan fokus saat mengerjakan soal matematika.
- Berlatihlah dengan soal-soal yang mirip dengan soal ujian.
Penerapan Konsep dalam Kehidupan Sehari-hari: Kunci Jawaban Matematika Kelas 9 Halaman 87 88

Konsep matematika yang dipelajari pada halaman 87-88 ternyata memiliki banyak aplikasi dalam kehidupan sehari-hari. Mulai dari menghitung uang belanja hingga menentukan rute perjalanan, konsep matematika berperan penting dalam membantu kita menyelesaikan berbagai masalah.
Penerapan Konsep Persamaan Linear
Persamaan linear, salah satu materi yang dibahas pada halaman 87-88, merupakan alat yang sangat berguna untuk menyelesaikan berbagai masalah dalam kehidupan nyata. Persamaan linear dapat digunakan untuk memodelkan hubungan antara dua variabel atau lebih, sehingga memungkinkan kita untuk memprediksi nilai satu variabel berdasarkan nilai variabel lainnya.
- Menghitung Biaya Produksi: Misalnya, jika sebuah toko ingin mengetahui total biaya produksi untuk membuat x unit produk, mereka dapat menggunakan persamaan linear. Jika biaya tetap produksi adalah Rp100.000 dan biaya variabel per unit adalah Rp5.000, maka total biaya produksi dapat dihitung dengan persamaan y = 5000 x + 100.000, di mana y adalah total biaya produksi dan x adalah jumlah unit produk.
- Menentukan Harga Jual: Persamaan linear juga dapat digunakan untuk menentukan harga jual produk. Misalnya, jika sebuah toko ingin menjual produk dengan keuntungan 20% dari harga beli, mereka dapat menggunakan persamaan linear y = 1,2 x, di mana y adalah harga jual dan x adalah harga beli.
Penerapan Konsep Sistem Persamaan Linear
Sistem persamaan linear merupakan konsep yang penting untuk menyelesaikan masalah yang melibatkan lebih dari satu variabel. Sistem persamaan linear dapat digunakan untuk menyelesaikan masalah yang melibatkan dua variabel atau lebih, sehingga memungkinkan kita untuk menemukan solusi yang memenuhi semua persamaan dalam sistem tersebut.
- Menentukan Jumlah Barang yang Dibeli: Misalnya, seorang ibu membeli 2 kg apel dan 3 kg jeruk dengan total harga Rp50.
000. Kemudian, ia membeli 1 kg apel dan 2 kg jeruk dengan total harga Rp30.
000. Untuk mengetahui berapa harga 1 kg apel dan 1 kg jeruk, kita dapat menggunakan sistem persamaan linear.Misalkan x adalah harga 1 kg apel dan y adalah harga 1 kg jeruk, maka sistem persamaan linearnya adalah:
2x + 3 y = 50.000
x + 2 y = 30.000Dengan menyelesaikan sistem persamaan linear ini, kita dapat mengetahui harga 1 kg apel dan 1 kg jeruk.
- Menentukan Jarak dan Kecepatan: Sistem persamaan linear juga dapat digunakan untuk menentukan jarak dan kecepatan. Misalnya, dua mobil bergerak saling berlawanan arah dengan kecepatan 60 km/jam dan 80 km/jam. Jika mereka bertemu setelah 2 jam, kita dapat menggunakan sistem persamaan linear untuk menentukan jarak awal antara kedua mobil tersebut.
Penerapan Konsep Pertidaksamaan Linear
Pertidaksamaan linear digunakan untuk menyelesaikan masalah yang melibatkan batasan atau syarat tertentu. Pertidaksamaan linear dapat digunakan untuk menentukan rentang nilai yang memenuhi syarat tertentu, sehingga memungkinkan kita untuk membuat keputusan yang tepat berdasarkan batasan yang ada.
- Menentukan Batasan Produksi: Misalnya, sebuah pabrik memiliki kapasitas produksi maksimal 100 unit produk per hari. Jika biaya produksi per unit adalah Rp10.000, maka pabrik tersebut dapat menghasilkan keuntungan maksimal Rp500.000 per hari. Untuk mengetahui berapa banyak unit produk yang harus diproduksi agar mencapai keuntungan maksimal, kita dapat menggunakan pertidaksamaan linear. Misalkan x adalah jumlah unit produk yang diproduksi, maka pertidaksamaan linearnya adalah:
10.000x ≤ 500.000
Dengan menyelesaikan pertidaksamaan linear ini, kita dapat mengetahui berapa banyak unit produk yang harus diproduksi agar mencapai keuntungan maksimal.
- Menentukan Batasan Pengeluaran: Pertidaksamaan linear juga dapat digunakan untuk menentukan batasan pengeluaran. Misalnya, seorang mahasiswa memiliki uang saku Rp500.000 per bulan. Jika biaya hidup per hari adalah Rp50.000, maka mahasiswa tersebut dapat menghabiskan maksimal Rp1.500.000 per bulan untuk keperluan lainnya. Untuk mengetahui berapa banyak uang yang dapat dihabiskan untuk keperluan lainnya, kita dapat menggunakan pertidaksamaan linear. Misalkan x adalah jumlah uang yang dapat dihabiskan untuk keperluan lainnya, maka pertidaksamaan linearnya adalah:
x ≤ 1.500.000
Dengan menyelesaikan pertidaksamaan linear ini, kita dapat mengetahui berapa banyak uang yang dapat dihabiskan untuk keperluan lainnya.
Dengan memahami konsep, menganalisis jenis soal, dan menerapkan strategi yang tepat, kamu akan lebih percaya diri dalam menghadapi soal-soal matematika di kelas 9. Ingat, belajar matematika tidak harus membosankan! Dengan mencari tahu dan mempraktikkan, kamu akan menemukan bahwa matematika bisa menjadi pelajaran yang menyenangkan dan bermanfaat.
FAQ dan Solusi
Apakah kunci jawaban ini cocok untuk semua buku matematika kelas 9?
Kunci jawaban ini khusus untuk buku matematika kelas 9 yang memuat materi pada halaman 87-88. Namun, konsep dan strategi yang dibahas dapat diterapkan pada buku matematika lainnya.
Bagaimana cara mengakses kunci jawaban ini?
Kunci jawaban ini tersedia dalam bentuk artikel yang dapat diakses secara online.
Apakah kunci jawaban ini memberikan solusi lengkap untuk semua soal?
Kunci jawaban ini memberikan panduan lengkap untuk memahami konsep dan strategi dalam menyelesaikan soal. Namun, solusi lengkap untuk setiap soal mungkin tidak selalu tersedia.