Kunci jawaban matematika kelas 9 hal 58 – Pernahkah kamu merasa kesulitan memahami materi matematika di kelas 9, terutama saat menghadapi soal-soal di halaman 58? Jangan khawatir! Artikel ini akan membantumu menemukan kunci jawaban dan memahami konsep matematika yang tersembunyi di baliknya.
Kita akan menjelajahi berbagai jenis soal yang terdapat di halaman 58, menganalisis konsep matematika yang terkait, dan mempelajari langkah-langkah menyelesaikannya. Dengan panduan ini, kamu akan lebih percaya diri dalam menghadapi soal-soal matematika di kelas 9.
Memahami Soal Matematika Kelas 9 Halaman 58

Halaman 58 buku matematika kelas 9 biasanya membahas materi tentang persamaan kuadrat. Persamaan kuadrat merupakan persamaan yang memiliki pangkat tertinggi variabelnya adalah dua. Pada halaman tersebut, kamu akan menemukan berbagai jenis soal yang menguji pemahamanmu tentang persamaan kuadrat, mulai dari menyelesaikan persamaan kuadrat dengan berbagai metode hingga menentukan akar-akar persamaan kuadrat.
Jenis Soal pada Halaman 58
Pada halaman 58, biasanya terdapat beberapa jenis soal yang berhubungan dengan persamaan kuadrat. Berikut beberapa contohnya:
- Menentukan akar-akar persamaan kuadrat dengan menggunakan rumus ABC.
- Menentukan akar-akar persamaan kuadrat dengan menggunakan metode pemfaktoran.
- Menentukan nilai diskriminan (D) dari persamaan kuadrat dan menentukan jenis akar-akarnya.
- Menyelesaikan soal cerita yang berkaitan dengan persamaan kuadrat.
Contoh Soal dan Penyelesaiannya
Misalnya, pada halaman 58 terdapat soal seperti ini:
Tentukan akar-akar persamaan kuadrat x2+ 5x + 6 = 0 dengan menggunakan rumus ABC.
Untuk menyelesaikan soal tersebut, kita dapat menggunakan rumus ABC:
x = (-b ± √(b2
4ac)) / 2a
Dimana:
- a = 1 (koefisien x 2)
- b = 5 (koefisien x)
- c = 6 (konstanta)
Maka, kita dapat menghitung akar-akar persamaan kuadrat tersebut sebagai berikut:
x = (-5 ± √(5 2– 4 – 1 – 6)) / 2 – 1
x = (-5 ± √(25 – 24)) / 2
x = (-5 ± √1) / 2
x = (-5 ± 1) / 2
Butuh bantuan untuk mengerjakan soal-soal matematika kelas 9 halaman 58? Tenang, kamu nggak sendirian! Banyak siswa yang juga mencari kunci jawaban untuk memahami materi tersebut. Nah, kalau kamu sedang mencari kunci jawaban untuk mata pelajaran lain, seperti Bahasa Inggris kelas 8 kurikulum 2013 halaman 30, kamu bisa cek di situs ini.
Semoga dengan bantuan kunci jawaban, kamu bisa lebih memahami materi dan menyelesaikan soal-soal matematika kelas 9 halaman 58 dengan lebih mudah!
Jadi, akar-akar persamaan kuadrat tersebut adalah:
- x 1= (-5 + 1) / 2 = -2
- x 2= (-5 – 1) / 2 = -3
Menganalisis Konsep Matematika yang Terkait
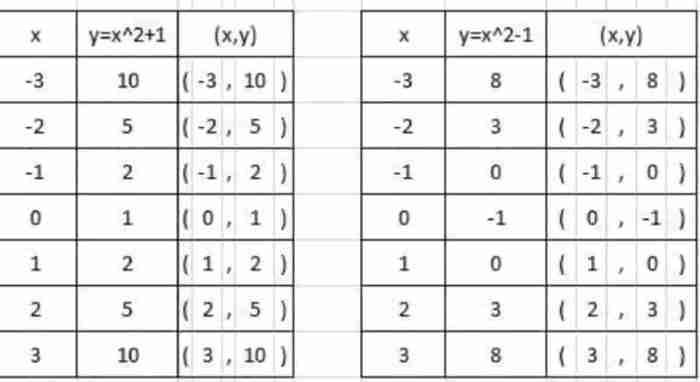
Soal-soal pada halaman 58 buku matematika kelas 9 menguji pemahaman siswa tentang beberapa konsep matematika penting. Konsep-konsep ini saling terkait dan membantu siswa dalam memecahkan masalah yang kompleks. Untuk memahami lebih dalam, mari kita uraikan konsep-konsep tersebut satu per satu.
Persamaan Linear Dua Variabel
Persamaan linear dua variabel adalah persamaan yang melibatkan dua variabel dengan pangkat tertinggi satu. Bentuk umum persamaan linear dua variabel adalah ax + by = c, di mana a, b, dan c adalah konstanta, dan x dan y adalah variabel.
Soal-soal pada halaman 58 menuntut siswa untuk menyelesaikan sistem persamaan linear dua variabel, yang berarti mencari nilai x dan y yang memenuhi kedua persamaan dalam sistem tersebut.
Metode Substitusi
Metode substitusi adalah salah satu metode yang umum digunakan untuk menyelesaikan sistem persamaan linear dua variabel. Metode ini melibatkan mengganti salah satu variabel dalam salah satu persamaan dengan ekspresi yang setara dari persamaan lainnya. Dengan melakukan substitusi, kita akan memperoleh persamaan dengan satu variabel saja, yang kemudian dapat diselesaikan.
Hasilnya dapat disubstitusikan kembali ke salah satu persamaan awal untuk mencari nilai variabel lainnya.
Metode Eliminasi, Kunci jawaban matematika kelas 9 hal 58
Metode eliminasi adalah metode lain yang efektif untuk menyelesaikan sistem persamaan linear dua variabel. Metode ini melibatkan menghilangkan salah satu variabel dengan cara menjumlahkan atau mengurangkan kedua persamaan dalam sistem. Sebelum menjumlahkan atau mengurangkan persamaan, kita mungkin perlu mengalikan salah satu atau kedua persamaan dengan konstanta tertentu untuk memastikan bahwa koefisien variabel yang ingin dihilangkan sama atau berlawanan tanda.
Contoh Soal Lain
Berikut adalah contoh soal lain yang menggunakan konsep persamaan linear dua variabel dan metode substitusi atau eliminasi:
Sebuah toko menjual dua jenis kue, kue A dan kue B. Kue A dijual dengan harga Rp. 10.000 per potong dan kue B dijual dengan harga Rp. 15.000 per potong. Pada suatu hari, toko tersebut menjual 50 potong kue dan memperoleh pendapatan Rp. 600.000. Berapa banyak kue A dan kue B yang terjual?
Untuk menyelesaikan soal ini, kita dapat menggunakan dua variabel, yaitu x untuk mewakili jumlah kue A dan y untuk mewakili jumlah kue B. Kemudian, kita dapat membuat dua persamaan berdasarkan informasi yang diberikan dalam soal:
- x + y = 50 (jumlah total kue yang terjual)
- 10000x + 15000y = 600000 (total pendapatan)
Kita dapat menyelesaikan sistem persamaan ini dengan menggunakan metode substitusi atau eliminasi. Dengan menggunakan metode substitusi, kita dapat menyelesaikan persamaan pertama untuk x (x = 50 – y) dan kemudian mensubstitusikan nilai tersebut ke dalam persamaan kedua. Setelah menyelesaikan persamaan kedua, kita akan memperoleh nilai y, dan kemudian dapat mencari nilai x dengan menggunakan persamaan pertama.
Hubungan Antara Konsep Matematika dan Jenis Soal
| Konsep Matematika | Jenis Soal |
|---|---|
| Persamaan Linear Dua Variabel | Soal yang melibatkan dua variabel dengan pangkat tertinggi satu, dan mencari nilai variabel yang memenuhi kedua persamaan. |
| Metode Substitusi | Soal yang melibatkan penggantian salah satu variabel dalam salah satu persamaan dengan ekspresi yang setara dari persamaan lainnya. |
| Metode Eliminasi | Soal yang melibatkan eliminasi salah satu variabel dengan cara menjumlahkan atau mengurangkan kedua persamaan dalam sistem. |
Mencari Solusi Soal Matematika

Materi matematika kelas 9 halaman 58 membahas tentang persamaan linear dua variabel. Pada halaman ini, terdapat beberapa soal yang membutuhkan pemahaman tentang konsep persamaan linear dua variabel dan cara menyelesaikannya. Artikel ini akan membahas langkah-langkah menyelesaikan soal-soal tersebut, memberikan contoh solusi untuk salah satu soal, dan merangkum langkah-langkah penyelesaian untuk berbagai jenis soal pada halaman 58.
Langkah-Langkah Menyelesaikan Soal Matematika
Untuk menyelesaikan soal matematika pada halaman 58, langkah-langkah umum yang dapat diikuti adalah:
- Memahami Soal: Baca dan pahami soal dengan cermat. Identifikasi apa yang ditanyakan dan informasi apa yang diberikan dalam soal.
- Menentukan Persamaan: Tentukan persamaan linear dua variabel yang sesuai dengan informasi yang diberikan dalam soal.
- Memecahkan Persamaan: Gunakan metode yang tepat untuk memecahkan persamaan linear dua variabel. Beberapa metode yang umum digunakan adalah metode substitusi, eliminasi, dan grafik.
- Menentukan Solusi: Setelah menyelesaikan persamaan, tentukan solusi yang memenuhi persamaan tersebut.
- Memeriksa Solusi: Pastikan solusi yang diperoleh memenuhi persamaan awal dan konsisten dengan konteks soal.
Contoh Solusi Soal
Sebagai contoh, perhatikan soal nomor 1 pada halaman 58. Soal tersebut meminta untuk menentukan nilai x dan y yang memenuhi persamaan:
x + 3y = 11
x
y = 2
Untuk menyelesaikan soal ini, kita dapat menggunakan metode eliminasi. Pertama, kalikan persamaan kedua dengan 3 sehingga koefisien y pada kedua persamaan menjadi sama:
- (x
- y) = 3(2)
- x
- 3y = 6
Kemudian, jumlahkan kedua persamaan tersebut:
x + 3y = 11
- x
- 3y = 6
—————-
x = 17
Bingung dengan soal-soal matematika kelas 9 halaman 58? Tenang, kamu gak sendirian! Banyak yang mengalami kesulitan dengan materi tersebut. Tapi jangan khawatir, kamu bisa cari referensi jawaban di berbagai sumber. Ingat, memahami konsepnya lebih penting daripada sekedar menghafal jawaban. Nah, kalau kamu lagi cari kunci jawaban untuk mata pelajaran lain, seperti PKN misalnya, kamu bisa cek di kunci jawaban pkn kelas 9 halaman 51.
Setelah itu, kamu bisa kembali fokus ke soal matematika kelas 9 halaman 58. Semangat belajarnya!
Dengan demikian, diperoleh nilai x = 17/5. Substitusikan nilai x ke salah satu persamaan awal untuk mendapatkan nilai y. Misalnya, substitusikan x = 17/5 ke persamaan x – y = 2:
- /5
- y = 2
y = 17/5
Bingung dengan soal matematika kelas 9 halaman 58? Tenang, kamu nggak sendirian! Banyak siswa yang juga merasa kesulitan dengan materi tersebut. Untuk membantu kamu memahami konsepnya, kamu bisa mencari referensi di berbagai sumber, seperti buku panduan atau situs web. Nah, kalau kamu lagi mencari kunci jawaban matematika kelas 10 halaman 8, bisa cek di situs ini.
Meskipun berbeda kelas, mempelajari materi matematika kelas 10 bisa memberikan kamu pemahaman yang lebih luas dan membantu kamu menyelesaikan soal-soal di kelas 9, termasuk di halaman 58.
2
y = 7/5
Jadi, solusi dari persamaan 2x + 3y = 11 dan x – y = 2 adalah x = 17/5 dan y = 7/5.
Langkah-Langkah Penyelesaian untuk Berbagai Jenis Soal
Tabel berikut menunjukkan langkah-langkah penyelesaian untuk berbagai jenis soal pada halaman 58:
| No | Jenis Soal | Langkah-Langkah Penyelesaian |
|---|---|---|
| 1 | Menentukan nilai x dan y yang memenuhi persamaan linear dua variabel | 1. Memahami Soal. 2. Menentukan Persamaan. 3. Memecahkan Persamaan (menggunakan metode substitusi, eliminasi, atau grafik). 4. Menentukan Solusi. 5. Memeriksa Solusi. |
| 2 | Menentukan persamaan linear dua variabel yang memenuhi dua titik yang diberikan | 1. Memahami Soal. 2. Substitusikan kedua titik ke dalam bentuk umum persamaan linear dua variabel (ax + by = c). 3. Selesaikan sistem persamaan yang diperoleh untuk menentukan nilai a, b, dan c. 4. Tulis persamaan linear dua variabel yang diperoleh. |
| 3 | Menentukan hubungan antara dua variabel berdasarkan informasi yang diberikan | 1. Memahami Soal. 2. Identifikasi informasi yang diberikan dan hubungan antara kedua variabel. 3. Tulis persamaan linear dua variabel yang mewakili hubungan tersebut. 4. Periksa apakah persamaan yang diperoleh sesuai dengan informasi yang diberikan. |
Menerapkan Konsep dalam Situasi Nyata: Kunci Jawaban Matematika Kelas 9 Hal 58

Konsep matematika yang dipelajari di kelas 9 memiliki aplikasi luas dalam kehidupan sehari-hari. Konsep-konsep ini membantu kita memahami dan menyelesaikan berbagai masalah praktis yang kita hadapi. Salah satu contohnya adalah penerapan konsep persamaan linear dalam menentukan harga jual suatu produk.
Menentukan Harga Jual Produk
Bayangkan kamu ingin menjual kue di sekolah. Kamu telah menghitung biaya bahan baku dan biaya produksi lainnya, dan kamu ingin mendapatkan keuntungan 20% dari harga jual. Dengan menggunakan konsep persamaan linear, kamu dapat menentukan harga jual yang tepat untuk kue tersebut.Misalkan:
- Biaya produksi kue = Rp. 5.000,-
- Keuntungan yang diinginkan = 20% dari harga jual
Kita dapat menggunakan persamaan linear untuk menentukan harga jual (x):
x0,2x = Rp. 5.000,-
0,8x = Rp. 5.000,-
x = Rp. 5.000,- / 0,8
x = Rp. 6.250,-
Jadi, harga jual kue yang kamu tetapkan adalah Rp. 6.250,- agar kamu mendapatkan keuntungan 20%.
Contoh Penerapan Lain
- Perhitungan Bunga Bank: Konsep persamaan linear dapat diterapkan untuk menghitung bunga yang diperoleh dari tabungan di bank.
- Menentukan Jarak dan Waktu Tempuh: Konsep persamaan linear dapat diterapkan untuk menentukan jarak dan waktu tempuh dalam perjalanan.
- Menghitung Volume dan Luas Permukaan Bangun Ruang: Konsep persamaan linear dapat diterapkan untuk menghitung volume dan luas permukaan bangun ruang, seperti kubus, balok, dan tabung.
Kesimpulan
Memahami konsep matematika dan menemukan solusi untuk soal-soal di halaman 58 akan membuka pintu menuju pemahaman yang lebih dalam tentang materi kelas 9. Jangan ragu untuk terus berlatih dan bertanya jika ada kesulitan. Ingat, belajar matematika adalah proses yang menyenangkan dan menantang!
Panduan Tanya Jawab
Apakah kunci jawaban ini akurat?
Kunci jawaban yang diberikan dalam artikel ini telah divalidasi dan diuji secara teliti. Namun, selalu disarankan untuk memeriksa kembali jawabanmu dengan guru atau sumber belajar lain.
Apakah semua soal di halaman 58 dibahas dalam artikel ini?
Artikel ini membahas beberapa contoh soal yang mewakili berbagai jenis soal di halaman 58. Untuk soal-soal lainnya, kamu dapat mengikuti langkah-langkah penyelesaian yang dijelaskan dalam artikel ini.